题目内容
19.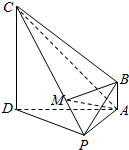 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).(1)若λ=$\frac{1}{4}$,求证:MB∥平面PAD;并求M到平面ABCD的距离;
(2)若λ=$\frac{1}{8}$,求二面角C-AB-M的余弦值.
分析 (1)根据线面平行的判定定理进行判断即可.
(2)建立空间直角坐标系,利用向量法进行求解即可.
解答 解:(1)若λ=$\frac{1}{4}$,则$\overrightarrow{PM}$=$\frac{1}{4}$$\overrightarrow{PC}$,
则PM=$\frac{1}{4}$PC,过M作ME∥AB交DPF于E,
则ME=$\frac{1}{4}$CD,EP=$\frac{1}{4}$DP
∵AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形AD=4AB=4,
∴AB=$\frac{1}{4}$CD,
则AB∥ME,且AB=ME,
即四边形ABME是平行四边形,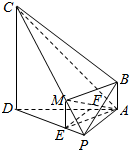
则MB∥AE,
∵MB?平面PAD,ME?平面PAD,
∴MB∥平面PAD;
∴M到平面ABCD的距离等于E到平面ABCD的距离;
过E作EF⊥AD于F,
则EF是E到平面ABCD的距离,
∵△PAD均为等腰三角形,AD=4,
∴AP=4,
∵EP=$\frac{1}{4}$DP,
∴EF=$\frac{1}{4}$AP=1,
即M到平面ABCD的距离等于1.
(2)以A为坐标原点,以AD,AP,AB分别为x,y,z轴,建立空间直角坐标系如图,
则AD=4,AB=1,AP=4,
若λ=$\frac{1}{8}$,则$\overrightarrow{PM}$=$\frac{1}{8}$$\overrightarrow{PC}$,
则A(0,0,0),B(0,0,1),D(4,0,0),P(0,4,0),C(4,0,4)
则$\overrightarrow{PC}$=(4,-4,4),
设M(a,b,c),
则由$\overrightarrow{PM}$=$\frac{1}{8}$$\overrightarrow{PC}$,
得(a,b-4,c)=($\frac{1}{2}$,-$\frac{1}{2}$,$\frac{1}{2}$),
则a=$\frac{1}{2}$,b=4-$\frac{1}{2}$=$\frac{7}{2}$,c=$\frac{1}{2}$,
即M($\frac{1}{2}$,$\frac{7}{2}$,$\frac{1}{2}$),
则$\overrightarrow{AB}$=(0,0,1),$\overrightarrow{AC}$=(4,0,4),$\overrightarrow{AM}$=($\frac{1}{2}$,$\frac{7}{2}$,$\frac{1}{2}$),
则平面CAB的一个法向量为$\overrightarrow{n}$=(0,1,0),
设$\overrightarrow{m}$=(x,y,z)为面ABM的一个法向量,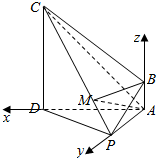
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AC}=0}\\{\overrightarrow{m}•\overrightarrow{AM}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{4x-4z=0}\\{\frac{1}{2}x+\frac{7}{2}y+\frac{1}{2}z=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x=z}\\{2x+7y=0}\end{array}\right.$,
令x=7,则z=7,y=-2,
即$\overrightarrow{m}$=(7,-2,7),
则cos<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{-2}{1×\sqrt{{7}^{2}+(-2)^{2}+{7}^{2}}}$=$-\frac{2}{\sqrt{102}}$=-$\frac{\sqrt{102}}{51}$,
∵二面角C-AB-M锐二面角,
∴二面角C-AB-M的余弦值为$\frac{\sqrt{102}}{51}$.
点评 本题综合考查空间中线面平行的判断和点到平面的距离的计算和空间角的计算,涉及二面角的平面角,利用向量法是解决空间角常用的方法,考查的知识面较广,难度中等.

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案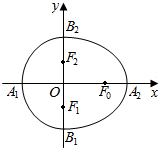 我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )
我们把由半椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(x>0)与半椭圆$\frac{{y}^{2}}{{b}^{2}}$+$\frac{{x}^{2}}{{c}^{2}}$=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2,a>b>c>0).如图,设点F0,F1,F2是相应椭圆的焦点,A1、A2和B1、B2是“果圆”与x,y轴的交点,若△F0F1F2是腰长为1的等腰直角三角形,则a,b的值分别为( )| A. | 5,4 | B. | $\frac{{\sqrt{7}}}{2},1$ | C. | $1,\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{6}}}{2},1$ |
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
| A. | $2<x<2\sqrt{2}$ | B. | $x<2\sqrt{2}$ | C. | $\sqrt{2}<x<2$ | D. | 0<x<2 |
