题目内容
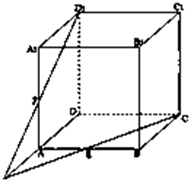在正方体ABCD-A1B1C1D1中，E为AB的中点，F为AA1的中点，求证：CE，D1F，DA三线共点．考点：平面的基本性质及推论
专题：空间位置关系与距离
分析：延长D1F、DA交于P，连结EP，由已知条件得△PAE≌△PAF，从而得到∠PEA+∠AEC=180°，由此能证明CE，D1F，DA三线共点于P．
解答：
解：延长D1F、DA交于P，连结EP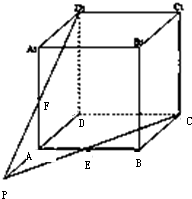
∵AE=AF，PA=PA，∠PAE=∠PAF=90°，
∴△PAE≌△PAF，
∴∠PFA=∠PEA，
∵∠PFA=∠PD1D，∠PD1D=∠DCE（∠A1D1F=∠BCE），
∴∠PEA=∠DCE，
又∵∠DCE+∠AEC=180°，
∴∠PEA+∠AEC=180°，
即点P、E、C共线，
∴CE，D1F，DA三线共点于P．
∵AE=AF，PA=PA，∠PAE=∠PAF=90°，
∴△PAE≌△PAF，
∴∠PFA=∠PEA，
∵∠PFA=∠PD1D，∠PD1D=∠DCE（∠A1D1F=∠BCE），
∴∠PEA=∠DCE，
又∵∠DCE+∠AEC=180°，
∴∠PEA+∠AEC=180°，
即点P、E、C共线，
∴CE，D1F，DA三线共点于P．
点评：本题考查三线共点的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目