题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsinA=3csinB,△ABC面积为
,cosB=
.
(1)求b的值;
(2)求cos(2B-A)的值.
| ||
| 2 |
| 2 |
| 3 |
(1)求b的值;
(2)求cos(2B-A)的值.
考点:两角和与差的余弦函数,正弦定理
专题:三角函数的求值,解三角形
分析:(1)利用同角三角函数间的关系及正弦定理、余弦定理即可求得b的值;
(2))利用同角三角函数间的关系可求得sinA,利用倍角公式可求得cos2B与sin2B,再由两角差的余弦可求得cos(2B-A)的值.
(2))利用同角三角函数间的关系可求得sinA,利用倍角公式可求得cos2B与sin2B,再由两角差的余弦可求得cos(2B-A)的值.
解答:
解:(1)在△ABC中,由正弦定理
=
得:bsinA=asinB,又bsinA=3csinB,
∴a=3c;
又cosB=
,
∴sinB=
=
,∵△ABC面积为
,
∴
acsinB=
×3c2×
=
,
∴c=1,a=3;
∴由余弦定理得:b2=a2+c2-2accosB=10-2×3×1×
=6,
解得:b=
.
(2)由余弦定理得cosA=
=
=-
,A∈(0,π),
∴sinA=
,
由cosB=
得:cos2B=2cos2B-1=-
(
<2B<π),sin2B=
,
∴cos(2B-A)=cos2BcosA+sin2BsinA=(-
)(-
)+
×
=
.
| a |
| sinA |
| b |
| sinB |
∴a=3c;
又cosB=
| 2 |
| 3 |
∴sinB=
| 1-cos2B |
| ||
| 3 |
| ||
| 2 |
∴
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 2 |
∴c=1,a=3;
∴由余弦定理得:b2=a2+c2-2accosB=10-2×3×1×
| 2 |
| 3 |
解得:b=
| 6 |
(2)由余弦定理得cosA=
| b2+c2-a2 |
| 2bc |
| 6+1-9 | ||
2×
|
| ||
| 6 |
∴sinA=
| ||
| 6 |
由cosB=
| 2 |
| 3 |
| 1 |
| 9 |
| π |
| 2 |
4
| ||
| 9 |
∴cos(2B-A)=cos2BcosA+sin2BsinA=(-
| 1 |
| 9 |
| ||
| 6 |
4
| ||
| 9 |
| ||
| 6 |
7
| ||
| 18 |
点评:本题考查倍角公式与两角差的余弦,考查同角三角函数间的关系的应用,突出考查运正弦定理与余弦定理的综合应用,考查运算能力,属于难题.

练习册系列答案
相关题目
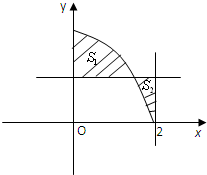 如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).
如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).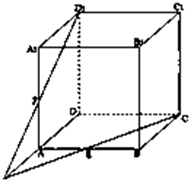 在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.
在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点. 如图,已知正三角形ABC的边长为6,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则
如图,已知正三角形ABC的边长为6,点D为边AC的中点,点E为边AB上离点A较近的三等分点,则