题目内容
已知圆C经过点A(-4,0),B(0,4),且圆心在直线y=x上,又直线l:y=kx+2与圆C相交于P,Q两点.
(Ⅰ)求圆C的方程;
(Ⅱ)若
•
=-8,求实数k的值;
(Ⅲ)过点(0,2)作直线l1与l垂直,且直线l1与圆C交于M,N两点,求四边形PMQN面积的最大值.
(Ⅰ)求圆C的方程;
(Ⅱ)若
| OP |
| OQ |
(Ⅲ)过点(0,2)作直线l1与l垂直,且直线l1与圆C交于M,N两点,求四边形PMQN面积的最大值.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(I)设圆心C(a,a),半径为r,利用|AC|=|BC|=r,建立方程,从而可求圆C的方程;
(II)利用向量的数量积公式,求得∠POQ=120°,计算圆心到直线l:kx-y+2=0的距离,即可求得实数k的值;
(III)设圆心O到直线l,l1的距离分别为d,d1,求得d12+d2=4,根据垂径定理和勾股定理得到,|PQ|=2
,|MN|=2
,再利用基本不等式,可求四边形PMQN面积的最大值.
(II)利用向量的数量积公式,求得∠POQ=120°,计算圆心到直线l:kx-y+2=0的距离,即可求得实数k的值;
(III)设圆心O到直线l,l1的距离分别为d,d1,求得d12+d2=4,根据垂径定理和勾股定理得到,|PQ|=2
| 16-d2 |
| 16-d12 |
解答:
解:(I)设圆心C(a,a),半径为r.
因为圆经过点A(-4,0),B(0,4),所以|AC|=|BC|=r,
所以
=
=r
解得a=0,r=4,
所以圆C的方程是x2+y2=16.
(II)因为
•
=-8,所以cos∠POQ=-
,所以∠POQ=120°,
所以圆心到直线l:kx-y+2=0的距离d=2,
又d=
,所以k=0.
(III)设圆心O到直线l,l1的距离分别为d,d1,四边形PMQN的面积为S.
因为直线l,l1都经过点(0,1),且l⊥l1,根据勾股定理,有d12+d2=4,
又根据垂径定理和勾股定理得到,|PQ|=2
,|MN|=2
所以S=
×2
×2
=2
≤2
=18
当且仅当d1=d时,等号成立,所以S的最大值为18.
因为圆经过点A(-4,0),B(0,4),所以|AC|=|BC|=r,
所以
| (a+4)2+a2 |
| a2+(a-4)2 |
解得a=0,r=4,
所以圆C的方程是x2+y2=16.
(II)因为
| OP |
| OQ |
| 1 |
| 2 |
所以圆心到直线l:kx-y+2=0的距离d=2,
又d=
| 2 | ||
|
(III)设圆心O到直线l,l1的距离分别为d,d1,四边形PMQN的面积为S.
因为直线l,l1都经过点(0,1),且l⊥l1,根据勾股定理,有d12+d2=4,
又根据垂径定理和勾股定理得到,|PQ|=2
| 16-d2 |
| 16-d12 |
所以S=
| 1 |
| 2 |
| 16-d2 |
| 16-d12 |
| 192+d12d2 |
| 192+4 |
当且仅当d1=d时,等号成立,所以S的最大值为18.
点评:本题考查圆的标准方程,考查向量的数量积,考查圆的性质,考查四边形面积的计算,考查基本不等式的运用,解题的关键是正确表示四边形的面积,属于中档题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
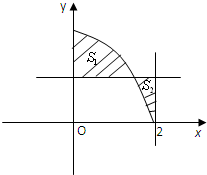 如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).
如图,已知S1为直线x=0,y=4-t2及y=4-x2所围成的面积,S2为直线x=2,y=4-t2及y=4-x2所围成图形的面积(t为常数).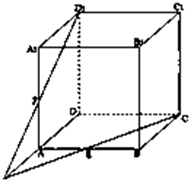 在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.
在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.
