题目内容
设a为常数,求数列a,2a2,3a2,…,nan的前n项和.
考点:数列的求和
专题:等差数列与等比数列
分析:设数列a,2a2,3a2,…,nan的前n项和为Sn,当a=0时,则Sn=0;当a=1时,Sn=
.若a≠0且a≠1时,利用错位相减法求解.
| n(n+1) |
| 2 |
解答:
解:设数列a,2a2,3a2,…,nan的前n项和为Sn,
当a=0时,则Sn=0.
当a=1时,Sn=1+2+3+…+n=
.
若a≠0且a≠1时,则Sn=a+2a2+3a3+4a4+…+nan,①
∴aSn=a2+2 a3+3 a4+…+nan+1,②
①-②,得(1-a) Sn=a+a2+a3+…+an-nan+1
=
-nan+1,
∴Sn=
-
,(a≠1)
若a=0,则Sn=0适合上式.
Sn=
.
∴数列a,2a2,3a2,…,nan的前n项和为
..
当a=0时,则Sn=0.
当a=1时,Sn=1+2+3+…+n=
| n(n+1) |
| 2 |
若a≠0且a≠1时,则Sn=a+2a2+3a3+4a4+…+nan,①
∴aSn=a2+2 a3+3 a4+…+nan+1,②
①-②,得(1-a) Sn=a+a2+a3+…+an-nan+1
=
| a(1-an) |
| 1-a |
∴Sn=
| a-an+1 |
| (1-a)2 |
| nan+1 |
| 1-a |
若a=0,则Sn=0适合上式.
Sn=
|
∴数列a,2a2,3a2,…,nan的前n项和为
|
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目

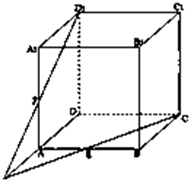 在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.
在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点,求证:CE,D1F,DA三线共点.