题目内容
已知点P(1+cosα,1-sinα),参数α∈R,点Q在曲线C:ρ=
上.
(1)求点P的轨迹方程和曲线C的直角坐标方程;
(2)求点P与点Q之间距离的最大值.
| 6 | ||||
|
(1)求点P的轨迹方程和曲线C的直角坐标方程;
(2)求点P与点Q之间距离的最大值.
考点:点的极坐标和直角坐标的互化,两点间的距离公式
专题:计算题,坐标系和参数方程
分析:(1)消参可得点P的轨迹方程,利用x=ρcosθ,y=ρsinθ,化为曲线C的直角坐标方程;
(2)由题意可得点Q在直线x+y-6=0上,点P在圆上,求出圆的圆心C到直线的距离,将此距离加上半径,即为所求.
(2)由题意可得点Q在直线x+y-6=0上,点P在圆上,求出圆的圆心C到直线的距离,将此距离加上半径,即为所求.
解答:
解:(1)点P的轨迹方程:由
得(x-1)2+(y-1)2=1,…(3分)
曲线C:ρ=
,可化为ρcosθ+ρsinθ-6=0
∴曲线C的直角坐标方程为:x+y-6=0…(5分)
(2)圆心到直线距离d=
=2
,
由圆心到直线距离加半径可得点P与点Q之间距离的最大值:|PQ|max=2
+1…(10分)
|
曲线C:ρ=
| 6 | ||||
|
∴曲线C的直角坐标方程为:x+y-6=0…(5分)
(2)圆心到直线距离d=
| |1+1-6| | ||
|
| 2 |
由圆心到直线距离加半径可得点P与点Q之间距离的最大值:|PQ|max=2
| 2 |
点评:本题主要考查把参数方程化为普通方程的方法,把极坐标方程化为直角坐标方程的方法,体现了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=ex-2x+a有零点,则实数a的取值范围是( )
| A、(-∞,2ln2-2] |
| B、[2ln2-2,+∞) |
| C、[2ln2,+∞) |
| D、[2ln2-2,2ln2] |
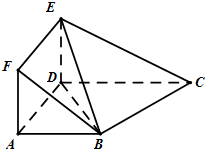 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,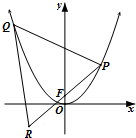 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+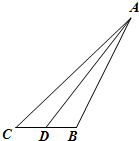 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-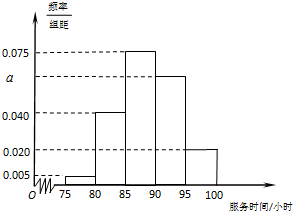 某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.