题目内容
已知函数f(x)=x3+ax2+b,
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程是y=x+1,求a,b的值;
(Ⅱ)若函数f(x)在区间(0,2)内单调递减.
(1)求a的取值集合A;
(2)对任意a∈A∩[-7,+∞)和x∈[0,4],有f(x)>a2恒成立,求实数b的取值范围.
(Ⅰ)若曲线y=f(x)在点(1,f(1))处的切线方程是y=x+1,求a,b的值;
(Ⅱ)若函数f(x)在区间(0,2)内单调递减.
(1)求a的取值集合A;
(2)对任意a∈A∩[-7,+∞)和x∈[0,4],有f(x)>a2恒成立,求实数b的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求出曲线y=f(x)的导数,利用在点(1,f(1))处的切线方程是y=x+1,即可求a,b的值;
(Ⅱ)(1)要使f(x)在(0,2)内单调递减,则f′(x)≤0在(0,2)内恒成立.即可求a的取值集合A;
(2)(i)当-7≤a≤-6时,f(x)在[0,4]上单调递减,函数的最小值>a2在a∈[-7,-6]上恒成立,求出b的范围;
(ii)当-6<a≤-3时,f(x)在[0,-
]上单调递减,[-
,4]上单调递增.有f(x)的最小值>a2恒成立,求实数b的取值范围.即可.
(Ⅱ)(1)要使f(x)在(0,2)内单调递减,则f′(x)≤0在(0,2)内恒成立.即可求a的取值集合A;
(2)(i)当-7≤a≤-6时,f(x)在[0,4]上单调递减,函数的最小值>a2在a∈[-7,-6]上恒成立,求出b的范围;
(ii)当-6<a≤-3时,f(x)在[0,-
| 2a |
| 3 |
| 2a |
| 3 |
解答:
解:(Ⅰ)f′(x)=3x2+2ax,
∴
,即
∴
-----------(4分)
(Ⅱ)(1)要使f(x)在(0,2)内单调递减,则f′(x)≤0在(0,2)内恒成立.
∴3x2+2ax≤0即a≤-
x在(0,2)上恒成立.
∴a≤-3即A=(-∞,-3]------------------------(7分)
(2)∵a∈A∩[-7,+∞)=[-7,-3]
(i)当-7≤a≤-6时,f(x)在[0,4]上单调递减,
∴fmin(x)=f(4)=64+16a+b>a2在a∈[-7,-6]上恒成立,
∴b>a2-16a-64在a∈[-7,-6]上恒成立∴b>97------------(10分)
(ii)当-6<a≤-3时,f(x)在[0,-
]上单调递减,[-
,4]上单调递增.
∴fmin(x)=f(-
)>a2在a∈(-6,-3]上恒成立.
即b>-
+a2在a∈(-6,-3]上恒成立
记g(a)=-
+a2a∈(-6,-3]
则g/(a)=-
+2a∈(-28,-10]
即g(a)在a∈(-6,-3]上单调递减.
∴g(a)>g(-6)=68,∴b>68-----------------------------------(14分)
综上所述,b>97-------------------------------------------------------(15分)
∴
|
|
∴
|
(Ⅱ)(1)要使f(x)在(0,2)内单调递减,则f′(x)≤0在(0,2)内恒成立.
∴3x2+2ax≤0即a≤-
| 3 |
| 2 |
∴a≤-3即A=(-∞,-3]------------------------(7分)
(2)∵a∈A∩[-7,+∞)=[-7,-3]
(i)当-7≤a≤-6时,f(x)在[0,4]上单调递减,
∴fmin(x)=f(4)=64+16a+b>a2在a∈[-7,-6]上恒成立,
∴b>a2-16a-64在a∈[-7,-6]上恒成立∴b>97------------(10分)
(ii)当-6<a≤-3时,f(x)在[0,-
| 2a |
| 3 |
| 2a |
| 3 |
∴fmin(x)=f(-
| 2a |
| 3 |
即b>-
| 4a3 |
| 27 |
记g(a)=-
| 4a3 |
| 27 |
则g/(a)=-
| 4a2 |
| 9 |
即g(a)在a∈(-6,-3]上单调递减.
∴g(a)>g(-6)=68,∴b>68-----------------------------------(14分)
综上所述,b>97-------------------------------------------------------(15分)
点评:本题主要考查利用导数研究函数的单调性等性质,及导数应用等基础知识,同时考查分类讨论等综合解题能力.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
执行如图所示的程序框图,若输入a1=2,a2=0,a3=1,a4=4,则计算机输出的结果是( )


| A、2 | B、0 | C、1 | D、4 |
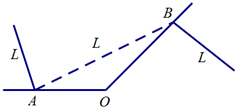 如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.
如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.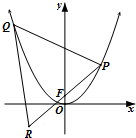 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+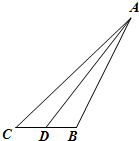 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-