题目内容
 已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<
已知如图为函数f(x)=2sin(ωx+φ)(ω>0,0<φ<| π |
| 2 |
(1)求f(x)的解析式及其单调递增区间;
(2)求函数g(x)=
| f(x)+2 | ||
f(x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,复合三角函数的单调性
专题:三角函数的图像与性质
分析:(1)由函数图象过点(0,1)可得φ=
,又ω
+φ=
,可得ω=2,可得函数解析式,整体法可得单调区间;
(2)由(1)知g(x)=y=
,变形可得sin(2x+
+φ)=
,由三角函数的有界性可得y的不等式,解不等式可得.
| π |
| 6 |
| 2π |
| 3 |
| 3π |
| 2 |
(2)由(1)知g(x)=y=
sin(2x+
| ||
cos(2x+
|
| π |
| 6 |
| y-1 | ||
|
解答:
解:(1)∵函数图象过点(0,1),
∴2sinφ=1,即sinφ=
,
又∵0<φ<
,∴φ=
又ω
+φ=
,∴ω=2,
∴f(x)=2sin(2x+
),
由2kπ-
≤2x+
≤2kπ+
可得kπ-
≤x≤kπ+
,
∴f(x)的单调递增区间为[kπ-
,kπ+
],k∈Z;
(2)由(1)知g(x)=
=
=
,
令y=
,
可得sin(2x+
)+1=ycos(2x+
)+y,
∴得sin(2x+
)-ycos(2x+
)=
sin(2x+
+φ)=y-1,
∴sin(2x+
+φ)=
,∴|
|≤1,
解得y≥0,即函数的值域为[0,+∞)
∴2sinφ=1,即sinφ=
| 1 |
| 2 |
又∵0<φ<
| π |
| 2 |
| π |
| 6 |
又ω
| 2π |
| 3 |
| 3π |
| 2 |
∴f(x)=2sin(2x+
| π |
| 6 |
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
∴f(x)的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
(2)由(1)知g(x)=
| f(x)+2 | ||
f(x+
|
sin(2x+
| ||||
sin(2x+
|
sin(2x+
| ||
cos(2x+
|
令y=
sin(2x+
| ||
cos(2x+
|
可得sin(2x+
| π |
| 6 |
| π |
| 6 |
∴得sin(2x+
| π |
| 6 |
| π |
| 6 |
| 1+y2 |
| π |
| 6 |
∴sin(2x+
| π |
| 6 |
| y-1 | ||
|
| y-1 | ||
|
解得y≥0,即函数的值域为[0,+∞)
点评:本题考查三角函数解析式的确定,涉及三角函数的单调性和有界性,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
双曲线
-
=1的离心率的值为( )
| y2 |
| 4 |
| x2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
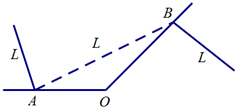 如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.
如图,某城市有一条公路从正西方AO通过市中心O后转向东北方OB,现要修筑一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,为了市民出行方便与城市环境问题,现要求市中心O到AB的距离为10km,设∠OAB=α.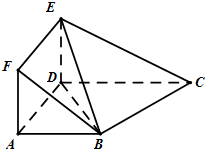 如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,
如图所示,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,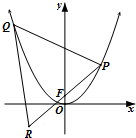 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+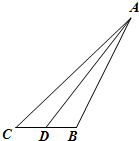 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-