题目内容
 某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.
某大学生在开学季准备销售一种文具盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如图所示.该同学为这个开学季购进了160盒该产品,以x(单位:盒,100≤x≤200)表示这个开学季内的市场需求量,y(单位:元)表示这个开学季内经销该产品的利润.(Ⅰ)根据直方图估计这个开学季内市场需求量x的众数和中位数(四舍五入取整数);
(Ⅱ)将y表示为x的函数;
(Ⅲ)根据直方图估计利润y不少于4800元的概率.
考点:频率分布直方图,古典概型及其概率计算公式
专题:算法和程序框图
分析:(Ⅰ)由频率直方图分别求出各组距内的频率,由此能求出这个开学季内市场需求量X的众数和中位数.
(Ⅱ)由已知条件推导出当100≤x≤160时,y=50x-(160-x)•30=80x-1800,当160<x≤200时,y=160×50=8000,由此能将Y表示为X的函数.
(Ⅲ)利用频率分布直方图能求出利润不少于4800元的概率.
(Ⅱ)由已知条件推导出当100≤x≤160时,y=50x-(160-x)•30=80x-1800,当160<x≤200时,y=160×50=8000,由此能将Y表示为X的函数.
(Ⅲ)利用频率分布直方图能求出利润不少于4800元的概率.
解答:
解:( I)众数为150,中位数为153 …4分
( II)∵每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元,
∴当100≤x≤160时,
y=50x-(160-x)•30=80x-1800,
当160<x≤200时,
y=160×50=8000,
y=
…8分
( III)由80x-4800≥4800得x≥120
估计利润y不少于4800元的概率P=
…12分.
( II)∵每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元,
∴当100≤x≤160时,
y=50x-(160-x)•30=80x-1800,
当160<x≤200时,
y=160×50=8000,
y=
|
( III)由80x-4800≥4800得x≥120
估计利润y不少于4800元的概率P=
| 9 |
| 10 |
点评:本题考查频率分布直方图的应用,考查函数解析式的求法,考查概率的估计,是中档题,解题时要注意频率分布直方图的合理运用.

练习册系列答案
相关题目
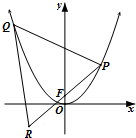 已知抛物线C:y=ax2,直线y=x+
已知抛物线C:y=ax2,直线y=x+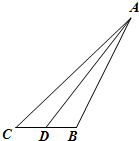 如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-
如图,在△ABC中,∠C=45°,D为BC中点,BC=2.记锐角∠ADB=α.且满足cosα=-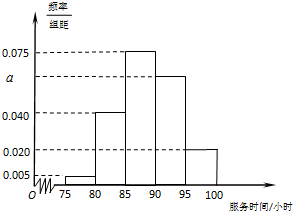 某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市规定,高三毕业生三年在校期间参加不少于80小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据为样本,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.