题目内容
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆C的标准方程.
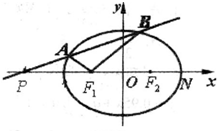
(Ⅱ)过点P(-2,0)作直线l与椭圆C交于A、B两点,求△AF1B的面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)利用过焦点垂直于长轴的弦长为
,焦点与短轴两端点构成等腰直角三角形,建立等式,求出a,b,可得椭圆C的标准方程.
(Ⅱ)设直线l:my=x+2(m≠0),代入椭圆方程,表示出△AF1B的面积,利用基本不等式,即可求出△AF1B的面积的最大值.
| 2 |
(Ⅱ)设直线l:my=x+2(m≠0),代入椭圆方程,表示出△AF1B的面积,利用基本不等式,即可求出△AF1B的面积的最大值.
解答:
解:(Ⅰ)∵过焦点垂直于长轴的弦长为
,焦点与短轴两端点构成等腰直角三角形,
∴b=c,
=
,
∴a=
,b=1,
∴椭圆C的标准方程为
+y2=1.
(Ⅱ)设直线l:my=x+2(m≠0),代入椭圆方程可得(m2+2)y2-4my+2=0,
△=(4m)2-8(m2+2)>0,可得m2>2,
设A(x1,y1),B(x2,y2),则y1+y2=
,y1•y2=
,
∴△AF1B的面积为S△PF1B-S△PF1A=
|PF1||y2-y1|=
|y2-y1|,
|y2-y1|=
=2
=2
≤2
=
,
当且仅当m2=6时,取等号,满足m2>2,
∴△AF1B的面积的最大值为
•
=
.
| 2 |
∴b=c,
| 2b2 |
| a |
| 2 |
∴a=
| 2 |
∴椭圆C的标准方程为
| x2 |
| 2 |
(Ⅱ)设直线l:my=x+2(m≠0),代入椭圆方程可得(m2+2)y2-4my+2=0,
△=(4m)2-8(m2+2)>0,可得m2>2,
设A(x1,y1),B(x2,y2),则y1+y2=
| 4m |
| m2+2 |
| 2 |
| m2+2 |
∴△AF1B的面积为S△PF1B-S△PF1A=
| 1 |
| 2 |
| 1 |
| 2 |
|y2-y1|=
(
|
|
|
|
| ||
| 2 |
当且仅当m2=6时,取等号,满足m2>2,
∴△AF1B的面积的最大值为
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查韦达定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、若“p∧q”为假命题,则p,q均为假命题 |
| B、“x>2”是“x2-3x+2>0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x+1<0”的否定是:“?x∈R 均有x2+x+1<0” |
| D、在△ABC中,若A是最大角,则“sin2B+sin2C<sin2A”是“△ABC为钝角三角形”的充要条件 |
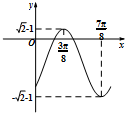 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<