题目内容
设f(x)=
(a>0)为奇函数,且|f(x)|min=2
,数列{an}满足如下关系a1=2,an+1=f(an)-an.
(Ⅰ)求f(x)的解析表达式;
(Ⅱ)证明:an+1>
(n∈N*);
(Ⅲ)令bn=
,研究数列{bn}的单调性.
| ax2+bx+1 |
| x+c |
| 2 |
(Ⅰ)求f(x)的解析表达式;
(Ⅱ)证明:an+1>
| 2n+1 |
(Ⅲ)令bn=
| an | ||
|
考点:数学归纳法,函数解析式的求解及常用方法,函数奇偶性的判断,综合法与分析法(选修)
专题:点列、递归数列与数学归纳法
分析:(Ⅰ)利用f(x)为奇函数,且|f(x)|min=2
,求出a,b,c即可的f(x)的解析表达式.
(Ⅱ)利用已知关系式,通过数学归纳法直接证明即可.
(Ⅲ)利用已知关系式通过化简
,利用放缩法以及基本不等式推出比值小于1,即可推出结果.
| 2 |
(Ⅱ)利用已知关系式,通过数学归纳法直接证明即可.
(Ⅲ)利用已知关系式通过化简
| bn+1 |
| bn |
解答:
解:(Ⅰ)由f(x)是奇函数,f(-x)+f(x)=0,得b=c=0,f(x)=ax+
,
∵a>0,
∴|f(x)|=|ax|+|
|≥2
=2
(当且仅当|ax|=|
|时取等号),
即|f(x)|min=2
,又|f(x)|min=2
,
∴a=2,故f(x)=2x+
.
(Ⅱ)an+1=f(an)-an=
+an,当n=1时,a1=2,a2=
+an=
>
不等式成立.
假设n=k时不等式成立,即:ak+1>
成立,
当n=k+1时,ak+22=ak+12+
+2>2k+3+
>2(k+1)+1,
∴ak+2>
,
∴n=k+1时成立,
综上由数学归纳法可知,an+1>
(n∈N*)恒成立;
(Ⅲ)
=
=(1+
)
<(1+
)
=(
)
=
=
<1.
故bn+1<bn.
| 1 |
| x |
∵a>0,
∴|f(x)|=|ax|+|
| 1 |
| x |
|ax||
|
| a |
| 1 |
| x |
即|f(x)|min=2
| a |
| 2 |
∴a=2,故f(x)=2x+
| 1 |
| x |
(Ⅱ)an+1=f(an)-an=
| 1 |
| an |
| 1 |
| an |
| 5 |
| 2 |
| 5 |
假设n=k时不等式成立,即:ak+1>
| 2k+1 |
当n=k+1时,ak+22=ak+12+
| 1 |
| ak+12 |
| 1 |
| ak+12 |
∴ak+2>
| 2(k+1)+1 |
∴n=k+1时成立,
综上由数学归纳法可知,an+1>
| 2n+1 |
(Ⅲ)
| bn+1 |
| bn |
an+1
| ||
an
|
=(1+
| 1 |
| an2 |
| ||
|
<(1+
| 1 |
| 2n+1 |
| ||
|
=(
| 2(n+1) |
| 2n+1 |
| ||
|
=
2
| ||
| 2n+1 |
=
| ||||||
n+
|
故bn+1<bn.
点评:本题考查数学归纳法以及放缩法的应用,函数的解析式的求法,考查计算能力以及逻辑推理能力.

练习册系列答案
相关题目
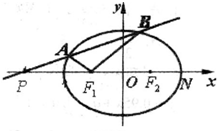 已知椭圆C:
已知椭圆C: 唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],
唐徕回中随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图,其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100],