题目内容
已知圆C:
(α为参数)与直线l:ρ(cosθ+sinθ)=2,则直线l截圆C所得的弦长为 .
|
考点:参数方程化成普通方程,点的极坐标和直角坐标的互化
专题:坐标系和参数方程
分析:把圆C的参数方程化为普通方程,直线l的极坐标方程化为普通方程,求出圆心(0,1)到直线的距离,即可求出直线l截圆C所得的弦长.
解答:
解:∵圆C的参数方程是
(α为参数),
化为普通方程是x2+(y-1)2=1;
又∵直线l:ρ(cosθ+sinθ)=2,
化为普通方程是x+y=2;
∴圆心(0,1)到直线的距离是
d=
=
,
∴直线l截圆C所得的弦长为
2×
=
.
故答案为:
.
|
化为普通方程是x2+(y-1)2=1;
又∵直线l:ρ(cosθ+sinθ)=2,
化为普通方程是x+y=2;
∴圆心(0,1)到直线的距离是
d=
| |1×0+1×1-2| | ||
|
| ||
| 2 |
∴直线l截圆C所得的弦长为
2×
12-(
|
| 2 |
故答案为:
| 2 |
点评:本题考查了参数方程与极坐标的应用问题,解题时应先把参数方程与极坐标方程化为普通方程,便于解答问题,是基础题.

练习册系列答案
相关题目
复数z=1+
的模为( )
| 1 |
| i |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
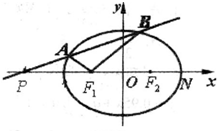 已知椭圆C:
已知椭圆C: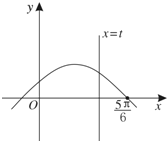 已知函数f(x)=
已知函数f(x)= 如图所示,在边长为3的正方形ABCD中,有一束光线从P点射出,到Q点反射,AP=1,BQ=1,之后会不断地被正方形的各边反射,当光线又回到点P时,
如图所示,在边长为3的正方形ABCD中,有一束光线从P点射出,到Q点反射,AP=1,BQ=1,之后会不断地被正方形的各边反射,当光线又回到点P时,