题目内容
下列说法正确的是（ ）
| A、若“p∧q”为假命题，则p，q均为假命题 |
| B、“x＞2”是“x2-3x+2＞0”的必要不充分条件 |
| C、命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R 均有x2+x+1＜0” |
| D、在△ABC中，若A是最大角，则“sin2B+sin2C＜sin2A”是“△ABC为钝角三角形”的充要条件 |
考点：命题的真假判断与应用
专题：综合题,推理和证明
分析：A，若“p∧q”为假命题，则p，q至少有一个假命题；
B，“x＞2”是“x2-3x+2＞0”的充分不必要条件；
C，命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R 均有x2+x+1≥0”；
D，利用正弦定理及余弦定理，即可判断．
B，“x＞2”是“x2-3x+2＞0”的充分不必要条件；
C，命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R 均有x2+x+1≥0”；
D，利用正弦定理及余弦定理，即可判断．
解答：
解：A，不正确，若“p∧q”为假命题，则p，q至少有一个假命题；
B，不正确，“x＞2”是“x2-3x+2＞0”的充分不必要条件；
C，不正确，命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R 均有x2+x+1≥0”；
D，正确，在△ABC中，若A是最大角，“sin2B+sin2C＜sin2A”，可得b2+c2＜a2，∴cosA＜0，∴“△ABC为钝角三角形”；“△ABC为钝角三角形”，A是最大角，则cosA＜0，∴b2+c2＜a2，“sin2B+sin2C＜sin2A”．
故选：D．
B，不正确，“x＞2”是“x2-3x+2＞0”的充分不必要条件；
C，不正确，命题“?x∈R使得x2+x+1＜0”的否定是：“?x∈R 均有x2+x+1≥0”；
D，正确，在△ABC中，若A是最大角，“sin2B+sin2C＜sin2A”，可得b2+c2＜a2，∴cosA＜0，∴“△ABC为钝角三角形”；“△ABC为钝角三角形”，A是最大角，则cosA＜0，∴b2+c2＜a2，“sin2B+sin2C＜sin2A”．
故选：D．
点评：本题考查命题的真假判断与应用，考查简易逻辑知识，考查学生分析解决问题的能力，知识综合性强．
练习册系列答案
灵星计算小达人系列答案
孟建平错题本系列答案
相关题目
已知f（x）是定义在[-1，1]上的奇函数，当x1≤x2时，f（x1）≤f（x2）．当x∈[0，1]时，2f(
)=f(x)，f（x）=1-f（1-x），则f(-
)+f(-
)+…+f(-
)+f(-
)=（ ）
| x |
| 5 |
| 150 |
| 2014 |
| 151 |
| 2014 |
| 170 |
| 2014 |
| 171 |
| 2014 |
A、-
| ||
| B、-5 | ||
| C、-6 | ||
D、-
|
设集合U={1，2，3，4，5}，A={2，3，5}，则∁UA=（ ）
| A、{5} |
| B、{1，4} |
| C、{2，3} |
| D、{2，3，5} |
下列各式中，函数的个数是（ ）
①y=1；②y=x2；③y=1-x；④y=
+
．
①y=1；②y=x2；③y=1-x；④y=
| x-2 |
| 1-x |
| A、4 | B、3 | C、2 | D、1 |
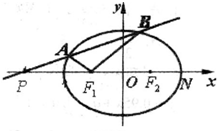已知椭圆C：