题目内容
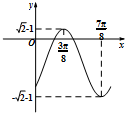 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<| π |
| 2 |
(1)求f(x)的解析式;
(2)若cosC=f(
| C |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦定理,余弦定理
专题:三角函数的图像与性质
分析:(1)通过函数图象,求出函数的最大值以及最小值的表达式,求出a,b.然后求出函数的周期,利用函数经过的特殊点,求出θ,即可求f(x)的解析式;
(2)利用cosC=f(
)+1,求出C的正弦函数值,然后利用三角形的面积公式求解△ABC的面积S.
(2)利用cosC=f(
| C |
| 2 |
解答:
(本小题满分13分)
解:(1)由图象可知:f(x)max=a-b=
-1,f(x)min=-a-b=-
-1,
得a=
,b=1;…(2分)
函数f(x)的最小正周期T=
=2(
-
)=π,得ω=2.…(3分)
由f(
)=
sin(2×
+θ)-1=
-1得sin(
+θ)=1…(4分)
∵|θ|<
,∴
+θ∈(
,
),
∴
+θ=
,θ=-
…(5分)
故f(x)=
sin(2x-
)-1 …(6分)
(2)由cosC=f(
)+1得,cosC=sinC-cosC,…(7分)
即cosC=
sinC …(8分)
又sin2C+cos2C=1,得sin2C=
,sinC=±
…(10分)
由0<C<π得,sinC=
,…(11分)
故S=
absinC=
…(13分)
解:(1)由图象可知:f(x)max=a-b=
| 2 |
| 2 |
得a=
| 2 |
函数f(x)的最小正周期T=
| 2π |
| ω |
| 7π |
| 8 |
| 3π |
| 8 |
由f(
| 3π |
| 8 |
| 2 |
| 3π |
| 8 |
| 2 |
| 3π |
| 4 |
∵|θ|<
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴
| 3π |
| 4 |
| π |
| 2 |
| π |
| 4 |
故f(x)=
| 2 |
| π |
| 4 |
(2)由cosC=f(
| C |
| 2 |
即cosC=
| 1 |
| 2 |
又sin2C+cos2C=1,得sin2C=
| 4 |
| 5 |
2
| ||
| 5 |
由0<C<π得,sinC=
2
| ||
| 5 |
故S=
| 1 |
| 2 |
| ||
| 5 |
点评:本题考查三角函数解析式的求法,三角函数的基本性质的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
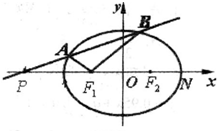 已知椭圆C:
已知椭圆C: