题目内容
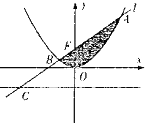 如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|BC|=
如图,过抛物线x2=2py(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|BC|=| 2 |
| 2 |
A、4
| ||
B、2
| ||
C、2
| ||
D、4
|
考点:定积分在求面积中的应用
专题:导数的概念及应用
分析:先确定积分的定义域,在确定积分函数,最后通过求定积分来求的相应的面积.
解答:
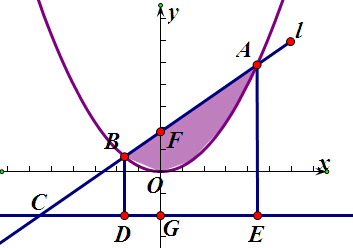 解:分别过点A,B作准线的垂线,分别交准线于点E,D,
解:分别过点A,B作准线的垂线,分别交准线于点E,D,
设|BF|=a,则由已知得:|BC|=
a,由定义得:|BD|=a,故∠BCD=45°,
在直角三角形ACE中,∵|AE|=4+2
,
∴|AC|=4
+4
∵|AF|=4+2
,
∴|CF|=2
,
∴|GF|=2
∴p=2,
∴x2=4y,
∴焦点F的坐标为(0,2),
∴直线l的方程为y=x+2,
由
,
解得x=2±2
,
∴直线AB与抛物线x2=4y(p>0)所围成的封闭图形的面积为S=
( x+2-
x2)dx=(
x2+2x-
x3)|
=4
故选:D
 解:分别过点A,B作准线的垂线,分别交准线于点E,D,
解:分别过点A,B作准线的垂线,分别交准线于点E,D,设|BF|=a,则由已知得:|BC|=
| 2 |
在直角三角形ACE中,∵|AE|=4+2
| 2 |
∴|AC|=4
| 2 |
∵|AF|=4+2
| 2 |
∴|CF|=2
| 2 |
∴|GF|=2
∴p=2,
∴x2=4y,
∴焦点F的坐标为(0,2),
∴直线l的方程为y=x+2,
由
|
解得x=2±2
| 3 |
∴直线AB与抛物线x2=4y(p>0)所围成的封闭图形的面积为S=
| ∫ | 2+2
2-2
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 12 |
2+2
2-2
|
| 3 |
故选:D
点评:定积分类的题先要弄清楚定积分的含义,运算的时候要弄清楚定积分的定义域和积分函数.

练习册系列答案
相关题目
四面体S-ABC中,已知SA⊥AB,AB⊥BC,|
|=3,|
|=4,|
|=5,|
|=
,则二面角S-AB-C的大小为( )
| SA |
| AB |
| BC |
| SC |
| 35 |
A、
| ||
B、
| ||
C、
| ||
D、
|
由6个座位连成一排,现有3人就坐,则恰有两个空座位相邻的不同坐法有( )
| A、36种 | B、48种 |
| C、72种 | D、96种 |
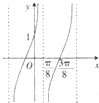 已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<
已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、kπ+
| ||||
D、
|
已知函数y=f(x)的值域是[1,4],则y=f(x-1)的值域是( )
| A、[1,4] |
| B、[1,5] |
| C、[0,3] |
| D、[2,5] |