题目内容
若函数f(x)=(k-2)x2+(k-1)x+3是偶函数,则f(x)的递增区间是 .
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:由函数f(x)是偶函数,可得f(-x)=f(x),求得k,再利用二次函数的单调性即可得出其单调区间.
解答:
解:∵函数f(x)=(k-2)x2+(k-1)x+3是偶函数,
∴f(-x)=f(x),∴(k-2)x2-(k-1)x+3=(k-2)x2+(k-1)x+3,
化为(k-1)x=0,此式对于任意实数x∈R都成立,
∴k-1=0,∴k=1.
∴f(x)=-x2+3,
∴函数f(x)的递增区间是(-∞,0].
故答案为:(-∞,0].
∴f(-x)=f(x),∴(k-2)x2-(k-1)x+3=(k-2)x2+(k-1)x+3,
化为(k-1)x=0,此式对于任意实数x∈R都成立,
∴k-1=0,∴k=1.
∴f(x)=-x2+3,
∴函数f(x)的递增区间是(-∞,0].
故答案为:(-∞,0].
点评:本题考查函数的奇偶性和单调性及运用,正确理解函数的奇偶性和单调性是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
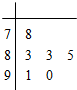 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:①中位数为84;
②众数为85;
③平均数为85;
④极差为12.
其中,正确说法的序号是( )
| A、①② | B、③④ | C、②④ | D、①③ |
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )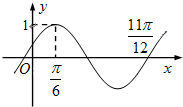
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
已知k∈[-2,1],则k的值使得过A(1,1)可以作两条直线与圆 x2+y2+kx-2y-
k=0相切的概率等于( )
| 5 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
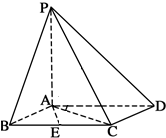 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.