题目内容
已知锐角A是△ABC的一个内角,a,b,c是三角形中各角的对应边,若sin2A-cos2A=
,则b+c与2a的大小关系为 .(填<或>或≤或≥或=)
| 1 |
| 2 |
考点:正弦定理
专题:解三角形
分析:已知等式利用二倍角的余弦函数公式化简,整理求出cos2A的值,确定出A的度数,设B=60°+x,0≤x<60°,则有C=60°-x,
<cosx≤1,表示出sinB+sinC,求出2sinA的值,即可做出判断.
| 1 |
| 2 |
解答:
解:∵锐角△ABC中,sin2A-cos2A=-cos2A=
,即cos2A=-
,
∴2A=120°,即A=60°,
设B=60°+x,0≤x<60°,则有C=60°-x,
<cosx≤1,
∵sinB+sinC=sin(60°+x)+sin(60°-x)=2sin60°cosx=
cosx,2sinA=2×
=
,
∴sinB+sinC≤2sinA,
由正弦定理化简得:b+c≤2a,
故答案为:≤
| 1 |
| 2 |
| 1 |
| 2 |
∴2A=120°,即A=60°,
设B=60°+x,0≤x<60°,则有C=60°-x,
| 1 |
| 2 |
∵sinB+sinC=sin(60°+x)+sin(60°-x)=2sin60°cosx=
| 3 |
| ||
| 2 |
| 3 |
∴sinB+sinC≤2sinA,
由正弦定理化简得:b+c≤2a,
故答案为:≤
点评:此题考查了正弦定理,二倍角的余弦函数公式,以及和差化积公式,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
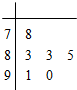 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,给出关于该同学数学成绩的以下说法:①中位数为84;
②众数为85;
③平均数为85;
④极差为12.
其中,正确说法的序号是( )
| A、①② | B、③④ | C、②④ | D、①③ |
把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设a=log
3,b=(
)0.2,c=2
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、a<c<b |
已知函数f(x)在R上满足f(x)=2f(-x)-x2则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、y=x |
| B、y=2x-1 |
| C、y=3x-2 |
| D、y=-2x+3 |
函数y=3 x2-3x+2,x∈[-1,2]的值域是( )
| A、R | |||||
B、[
| |||||
| C、[9,243] | |||||
| D、[3,+∞) |
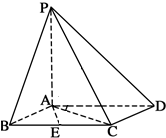 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.