题目内容
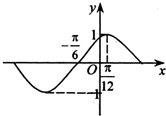 函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<
函数f(x)=sin(ωx+ϕ)(ω>0,|ϕ|<| π |
| 2 |
| π |
| 4 |
A、[kπ-
| ||||
B、[kπ+
| ||||
C、[kπ-
| ||||
D、[kπ+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的求值,三角函数的图像与性质
分析:首先根据函数的图象求A、ω、Φ的值,进一步确定函数的解析式,最后利用整体思想求函数的单调递增区间.
解答:
解:根据函数的图象:
=
+
=
,
∴T=π,
∴ω=2;
当x=
时,f(
)=1求得:Φ=
,
所以:f(x)=sin(2x+
),
将y=f(x)的图象向右平移
个单位后得到函数y=g(x)=sin(2x-
),
令:2kπ-
≤2x-
≤2kπ+
(k∈Z),
kπ-
≤x≤kπ+
(k∈Z),
故函数的递增区间为:[kπ-
,kπ+
](k∈Z),
故选:A.
| T |
| 4 |
| π |
| 12 |
| π |
| 6 |
| π |
| 4 |
∴T=π,
∴ω=2;
当x=
| π |
| 12 |
| π |
| 12 |
| π |
| 3 |
所以:f(x)=sin(2x+
| π |
| 3 |
将y=f(x)的图象向右平移
| π |
| 4 |
| π |
| 6 |
令:2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
kπ-
| π |
| 6 |
| π |
| 3 |
故函数的递增区间为:[kπ-
| π |
| 6 |
| π |
| 3 |
故选:A.
点评:本题考查的知识要点:根据函数的图象求A、ω、Φ的值,确定函数的解析式,利用整体思想求函数的单调递增区间.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知坐标原点O在圆x2+y2-x+y+m=0外,则m的取值范围是( )
A、0<m<
| ||
B、m<
| ||
C、m≤
| ||
| D、m>0 |
函数f(x)=ax2+bx+5满足条件f(-1)=f(3),则f(2)的值为( )
| A、5 | B、6 |
| C、8 | D、与a,b的值有关 |
把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设a=log
3,b=(
)0.2,c=2
,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、a<c<b |
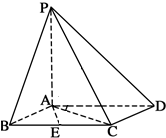 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.