题目内容
12.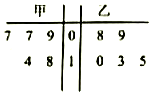 如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
如图是甲、乙两名篮球运动员在五场比赛中所得分数的茎叶图,则在这五场比赛中得分较为稳定(方差较小)的那名运动员的得分的方差为$\frac{34}{5}$.
分析 根据茎叶图中的数据求出甲、乙二人的平均数,再根据方差的定义得出乙的方差较小,求出乙的方差即可.
解答 解:根据茎叶图中的数据,计算甲的平均数为$\overline{{x}_{1}}$=$\frac{1}{5}$×(7+7+9+14+18)=11,
乙的平均数为$\overline{{x}_{2}}$=$\frac{1}{5}$×(8+9+10+13+15)=11;
根据茎叶图中的数据知乙的成绩波动性小,较为稳定(方差较小),
计算乙成绩的方差为:
s2=$\frac{1}{5}$×[(8-11)2+(9-11)2+(10-11)2+(13-11)2+(15-11)2]=$\frac{34}{5}$.
故答案为:$\frac{34}{5}$.
点评 本题考查了茎叶图、平均数与方差的应用问题,是基础题.

练习册系列答案
相关题目
3.已知数列{an}的前n项和为Sn,且${a_1}=1,{a_{n+1}}•{a_n}={2^n}(n∈{N^*})$,则S2016=( )
| A. | 3•21008-3 | B. | 22016-1 | C. | 22009-3 | D. | 22008-3 |
4.已知${({2x-3})^4}={a_0}+{a_1}(x-2)+{a_2}{(x-2)^2}+{a_3}{(x-2)^3}+{a_4}{(x-2)^4}$,则a2=( )
| A. | 24 | B. | 56 | C. | 80 | D. | 216 |
1.若P为可行域$\left\{\begin{array}{l}x≥-1\\ y≤2\\ 2x-y+2≤0\end{array}\right.$内的一点,过P的直线l与圆O:x2+y2=7交于A,B两点,则|AB|的最小值为( )
| A. | $2\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
 如图,圆O的弦AB,MN交于点C,且A为弧MN的中点,点D在弧BM上,若∠ACN=3∠ADB,求∠ADB的度数.
如图,圆O的弦AB,MN交于点C,且A为弧MN的中点,点D在弧BM上,若∠ACN=3∠ADB,求∠ADB的度数.