题目内容
6．已知实数x、y满足$\left\{\begin{array}{l}1≤x-y≤2\\ 2≤x+y≤4\end{array}\right.$，则z=4x-2y的最大值为（ ）| A． | 3 | B． | 5 | C． | 10 | D． | 12 |
分析 作出不等式组对应的平面区域，利用目标函数的几何意义，利用平移法进行求解即可．
解答 
解：作出实数x、y满足$\left\{\begin{array}{l}1≤x-y≤2\\ 2≤x+y≤4\end{array}\right.$的可行域，如图：$\left\{\begin{array}{l}{x-y=2}\\{x+y=4}\end{array}\right.$解得A（3，1），
作出直线l：4x-2y=0，平移直线l，当它过点A（3，1）时，z=4x-2y取得最大值10．
故选：C．
点评 本题主要考查线性规划的应用，根据条件结合目标函数的几何意义，利用平移法是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
17．已知集合A={x|y=ln（x-1）}，B={x|-1＜x＜2}，则（∁RA）∩B=（ ）
| A． | （-1，1） | B． | （-1，2） | C． | （-1，1] | D． | （1，2） |
14．如图，已知$\overrightarrow{AB}=a$，$\overrightarrow{AC}=b$，$\overrightarrow{DC}=3\overrightarrow{BD}$，$\overrightarrow{AE}=2\overrightarrow{EC}$，则$\overrightarrow{DE}$=（ ）
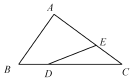
| A． | $\frac{3}{4}b-\frac{1}{3}a$ | B． | $\frac{5}{12}a-\frac{3}{4}b$ | C． | $\frac{3}{4}a-\frac{1}{3}b$ | D． | $\frac{5}{12}b-\frac{3}{4}a$ |
1．A、B为两个非空集合，定义集合A-B={x|x∈A且x∉B}，若A={-2，-1，0，1，2}，B={x|（x-1）（x+2）＜0}，则A-B=（ ）
| A． | {2} | B． | {1，2} | C． | {-2，1，2} | D． | {-2，-1，0} |
18．已知sin2α=$\frac{1}{4}$，则${sin^2}（α+\frac{π}{4}）$=（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{3}{8}$ | C． | $\frac{5}{8}$ | D． | $\frac{2}{3}$ |
15．某班级为了进行户外拓展游戏，组成红、蓝、黄3个小队．甲、乙两位同学各自等可能地选择其中一个小队，则他们选到同一小队的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |