题目内容
已知△ABC的内角A,B,C的对边分别为a,b,c,若cosA=
,sinC=3sinB,且S△ABC=
,则b=( )
| 1 |
| 3 |
| 2 |
| A、1 | ||
B、2
| ||
C、3
| ||
| D、3 |
考点:正弦定理
专题:三角函数的求值
分析:由cosA的值,利用同角三角函数间的基本关系求出sinA的值,利用正弦定理化简sinC=3sinB,再利用三角形面积公式列出关系式,将sinA,已知面积,以及表示出的c代入计算即可求出b的值.
解答:
解:∵cosA=
,A为三角形内角,
∴sinA=
=
,
由正弦定理化简sinC=3sinB,得c=3b,
∵S△ABC=
bcsinA=
3b2•
=
,
∴b=1.
故选:A.
| 1 |
| 3 |
∴sinA=
| 1-cos2A |
2
| ||
| 3 |
由正弦定理化简sinC=3sinB,得c=3b,
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| 2 |
∴b=1.
故选:A.
点评:此题考查了正弦定理,三角形面积公式,以及同角三角函数间的基本关系,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
 已知数列{an}的各项均为正数,执行程序框图(如图),当k=4时,S=
已知数列{an}的各项均为正数,执行程序框图(如图),当k=4时,S=| 1 |
| 3 |
| A、2012 | B、2013 |
| C、2014 | D、2015 |
设全集U={x|0<x<2},集合A={x|0<x≤1},则集合∁UA=( )
| A、(0,1) |
| B、(0,1] |
| C、(1,2) |
| D、[1,2) |
将一颗骰子连续抛掷三次,已知它落地时向上的点数恰好依次成等差数列,那么这三次抛掷向上的点数之和为12的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知直线
x+y+m=0与圆x2+y2=9交于A,B两点,则与向量
+
(O为坐标原点)共线的一个向量为( )
| 3 |
| OA |
| OB |
A、(1,-
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(1,-
|
 如图,矩形ABCD和矩形ABEF中,矩形ABEF可沿AB任意翻折,AF=AD,M、N分别在AE、DB上运动,当F、A、D不共线,M、N不与A、D重合,且AM=DN时,有( )
如图,矩形ABCD和矩形ABEF中,矩形ABEF可沿AB任意翻折,AF=AD,M、N分别在AE、DB上运动,当F、A、D不共线,M、N不与A、D重合,且AM=DN时,有( )| A、MN∥平面FAD |
| B、MN与平面FAD相交 |
| C、MN⊥平面FAD |
| D、MN与平面FAD可能平行,也可能相交 |
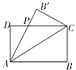 某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为
某制冷设备厂设计生产一种长方形薄板,如图所示,长方形ABCD(AB>AD)的周长为4米,沿AC折叠使B到B′位置,AB′交DC于P.研究发现当ADP的面积最大时最节能,则最节能时长方形ABCD的面积为