题目内容
把一颗骰子投掷两次,观察出现的点数,并记第一次出现的点数为a,第二次出现的点数为b.试就方程组
解答下列问题:
(Ⅰ)求方程组没有解的概率;
(Ⅱ)求以方程组的解为坐标的点在第四象限的概率.
|
(Ⅰ)求方程组没有解的概率;
(Ⅱ)求以方程组的解为坐标的点在第四象限的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)利用分布计数原理求出骰子投掷2次所有的结果,通过解二元一次方程组判断出方程组有唯一解的条件,求出满足该条件的结果个数,利用古典概型的概率公式求出方程组只有一个解的概率;
(Ⅱ)解方程组
,根据条件确定a,b的范围,从而确定满足该条件的结果个数利用古典概型的概率公式求出方程组只有一个解的概率.
(Ⅱ)解方程组
|
解答:
解:(Ⅰ)由题意知,(a,b)的可能共有36组,
方法1:若方程没有解,则
=
,即b=2a
(方法2:带入消元得(b-2a)y=3-2a,因为3-2a≠0,所以当 b=2a时方程组无解)
∴符合条件的数组为(1,2),(2,4),(3,6),
∴p=
=
,故方程组没有解的概率为
.
(Ⅱ)由方程组
得
,
若b>2a,则有
即a=2,3,4,5,6,b=4,5,6,
符合条件的数组有(2,5),(2,6)共有2个,
若b<2a,则有
即b=1,2,a=1
符合条件的数组有(1,1)共1个,
∴概率为p=
=
,
即以方程组的解为坐标的点在第四象限的概率为
.
方法1:若方程没有解,则
| a |
| 1 |
| b |
| 2 |
(方法2:带入消元得(b-2a)y=3-2a,因为3-2a≠0,所以当 b=2a时方程组无解)
∴符合条件的数组为(1,2),(2,4),(3,6),
∴p=
| 3 |
| 36 |
| 1 |
| 12 |
| 1 |
| 12 |
(Ⅱ)由方程组
|
|
若b>2a,则有
|
符合条件的数组有(2,5),(2,6)共有2个,
若b<2a,则有
|
符合条件的数组有(1,1)共1个,
∴概率为p=
| 1+2 |
| 36 |
| 1 |
| 12 |
即以方程组的解为坐标的点在第四象限的概率为
| 1 |
| 12 |
点评:本题考查古典概型及其概率计算公式的应用,求某个事件的概率,应该先判断出事件的概型,再选择合适的概率公式求出事件的概率,属于中档题.

练习册系列答案
相关题目
 已知向量
已知向量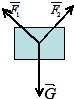 甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为
甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为