题目内容
为了研究某种细菌随时间x变化的繁殖个数,收集数据如下:
(1)作出这些数据的散点图;
(2)求出y对x的回归方程.
| 天数x | 1 | 2 | 3 | 4 | 5 | 6 |
| 繁殖个数y | 6 | 12 | 25 | 49 | 95 | 190 |
(2)求出y对x的回归方程.
考点:线性回归方程,散点图
专题:计算题,概率与统计
分析:(1)根据收集数据,可得数据的散点图;
(2)由散点图看出样本点分布在一条指数型曲线y=cebx(c>0)的周围,则lny=bx+lnc.变换后的样本点分布在一条直线附近,因此可以用线性回归方程来拟合,即可求出y对x的回归方程.
(2)由散点图看出样本点分布在一条指数型曲线y=cebx(c>0)的周围,则lny=bx+lnc.变换后的样本点分布在一条直线附近,因此可以用线性回归方程来拟合,即可求出y对x的回归方程.
解答:
解:(1)作出散点图如图1所示.
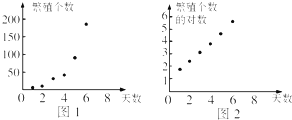
(2)由散点图看出样本点分布在一条指数型曲线y=cebx(c>0)的周围,则lny=bx+lnc.
相应的散点图如图2.
从图2可以看出,变换后的样本点分布在一条直线附近,因此可以用线性回归方程来拟合.
由表中数据得到线性回归方程为z=0.69x+1.115.
因此细菌的繁殖个数对温度的非线性回归方程为y=e0.69x+1.115.

(2)由散点图看出样本点分布在一条指数型曲线y=cebx(c>0)的周围,则lny=bx+lnc.
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| z | 1.79 | 2.48 | 3.22 | 3.89 | 4.55 | 5.25 |
从图2可以看出,变换后的样本点分布在一条直线附近,因此可以用线性回归方程来拟合.
由表中数据得到线性回归方程为z=0.69x+1.115.
因此细菌的繁殖个数对温度的非线性回归方程为y=e0.69x+1.115.
点评:本题考查线性回归方程,考查散点图,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
经平面外一点和平面内一点与平面α垂直的平面有( )
| A、1个 | B、0 个 |
| C、无数个 | D、1个或无数个 |
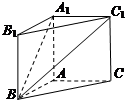 在直三棱柱(侧棱垂直底面)ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°.
在直三棱柱(侧棱垂直底面)ABC-A1B1C1中,AB=AC=1,∠BAC=90°,且异面直线A1B与B1C1所成的角等于60°.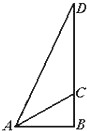 如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30m,在地面上有一点A,测得A、C间的距离为50米,从点A观测电视发射塔的视角为45°(∠CAD=45°),求这座电视发射塔的高度.
如图,某城市的电视发射塔CD建在市郊的小山上,小山的高BC为30m,在地面上有一点A,测得A、C间的距离为50米,从点A观测电视发射塔的视角为45°(∠CAD=45°),求这座电视发射塔的高度.