题目内容
某校为宣传县教育局提出的“教育发展,我的责任”教育实践活动,要举行一次以“我为教育发展做什么”为主题的演讲比赛,比赛分为初赛、复赛、决赛三个阶段进行,已知某选手通过初赛、复赛、决赛的概率分别是
,
,
,且各阶段通过与否相互独立.
(Ⅰ)求该选手在复赛阶段被淘汰的概率;
(Ⅱ)设该选手在比赛中比赛的次数为ξ,求ξ的分布列、数学期望和方差.
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅰ)求该选手在复赛阶段被淘汰的概率;
(Ⅱ)设该选手在比赛中比赛的次数为ξ,求ξ的分布列、数学期望和方差.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)记“该选手通过初赛”为事件A,“该选手通过复赛”为事件B,“该选手通过决赛”为事件C,则P(A)=
,P(B)=
,P(C)=
.由此能求出该选手在复赛阶段被淘汰的概率.
(Ⅱ)ξ可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列、数学期望和方差.
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
(Ⅱ)ξ可能取值为1,2,3,分别求出相应的概率,由此能求出ξ的分布列、数学期望和方差.
解答:
解:(Ⅰ)记“该选手通过初赛”为事件A,
“该选手通过复赛”为事件B,
“该选手通过决赛”为事件C,
则P(A)=
,P(B)=
,P(C)=
.
那么该选手在复赛阶段被淘汰的概率是:
p=p(A
)=P(A)P(
)=
×(1-
)=
.…(4分)
(Ⅱ)ξ可能取值为1,2,3.…(5分)P(ξ=1)=P(
)=1-
=
,P(ξ=2)=P(A
)=P(A)P(
)=
×(1-
)=
,P(ξ=3)=P(AB)=P(A)P(B)=
×
=
.…(8分)
ξ的分布列为
Eξ=1×
+2×
+3×
=
.…(10分)Dξ=(1-
)2×
+(2-
)2×
+(3-
)2×
=
.…(12分)
“该选手通过复赛”为事件B,
“该选手通过决赛”为事件C,
则P(A)=
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
那么该选手在复赛阶段被淘汰的概率是:
p=p(A
. |
| B |
. |
| B |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
(Ⅱ)ξ可能取值为1,2,3.…(5分)P(ξ=1)=P(
. |
| A |
| 2 |
| 3 |
| 1 |
| 3 |
. |
| B |
. |
| B |
| 2 |
| 3 |
| 1 |
| 3 |
| 4 |
| 9 |
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 9 |
ξ的分布列为
| ξ | 1 | 2 | 3 | ||||||
P |
|
|
|
| 1 |
| 3 |
| 4 |
| 9 |
| 2 |
| 9 |
| 17 |
| 9 |
| 17 |
| 9 |
| 1 |
| 3 |
| 17 |
| 9 |
| 4 |
| 9 |
| 17 |
| 9 |
| 2 |
| 9 |
| 44 |
| 81 |
点评:本题考查概率的求法,考查离散型随机变量的分布列、数学期望、方差的求法,解题时要认真审题,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
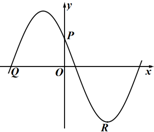 如图,点P(0,
如图,点P(0,