题目内容
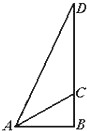如图，某城市的电视发射塔CD建在市郊的小山上，小山的高BC为30m，在地面上有一点A，测得A、C间的距离为50米，从点A观测电视发射塔的视角为45°（∠CAD=45°），求这座电视发射塔的高度．考点：解三角形的实际应用
专题：计算题,解三角形
分析：根据勾股定理求得AB，进而求得tan∠CAB，再通过tan∠DAB=tan（∠DAC+∠CAB）利用正切两角和公式，求得tan∠DAB，再通过tan∠DAB和AB，求得BD，进而求得DC．
解答：
解：根据勾股定理可知AB=
=40，
∴tan∠CAB=
，
∴tan∠DAB=tan（∠DAC+∠CAB）=
=7，
∴BD=ABtan∠DAB=7×40=280，
∴CD=BD-BC=250．
| 502-302 |
∴tan∠CAB=
| 3 |
| 4 |
∴tan∠DAB=tan（∠DAC+∠CAB）=
1+
| ||
1-
|
∴BD=ABtan∠DAB=7×40=280，
∴CD=BD-BC=250．
点评：本题主要考查了三角形的实际应用．属基础题．
练习册系列答案
相关题目
设a、b是不同的两条直线，α、β是不同的两个平面，分析下列命题，其中正确的是（ ）
| A、a⊥α，b?β，a⊥b⇒α⊥β |
| B、α∥β，a⊥α，b∥β⇒a⊥b |
| C、α⊥β，a⊥α，b∥β⇒a⊥b |
| D、α⊥β，α∩β=a，a⊥b⇒b⊥β |
在空间中，下列命题正确的是（ ）
| A、若两个平面有一个公共点，则它们必有无数个公共点 |
| B、任意三点都可以确定一个平面 |
| C、分别在不同平面内的两条直线叫异面直线 |
| D、垂直于同一条直线的两条直线互相平行 |
已知函数y=
sin（x+
），当y取得最小值时，tanx等于（ ）
| 2 |
| π |
| 4 |
| A、1 | ||||
| B、-1 | ||||
C、
| ||||
D、-
|