题目内容
过曲线C1:
-
=1(a>0,b>0)的左焦点F作曲线C2:x2+y2=a2的切线,设切点为M,延长FM交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若点M为线段FN的中点,则曲线C1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:双曲线的右焦点的坐标为(c,0),利用O为FF'的中点,M为FN的中点,可得OM为△NFF'的中位线,从而可求|NF|,再设N(x,y) 过点F作x轴的垂线,由勾股定理得出关于a,c的关系式,最后即可求得离心率.
解答:
解:设双曲线的右焦点为F',则F'的坐标为(c,0)
因为曲线C1与C3有一个共同的焦点,所以y2=4cx
因为O为FF'的中点,M为FN的中点,所以OM为△NFF'的中位线,
所以OM∥PF'
因为|OM|=a,所以|NF'|=2a
又NF'⊥NF,|FF'|=2c 所以|NF|=2b
设N(x,y),则由抛物线的定义可得x+c=2a,
∴x=2a-c
过点F作x轴的垂线,点N到该垂线的距离为2a
由勾股定理 y2+4a2=4b2,即4c(2a-c)+4a2=4(c2-a2)
得e2-e-1=0,
∴e=
.
故选:D.
因为曲线C1与C3有一个共同的焦点,所以y2=4cx
因为O为FF'的中点,M为FN的中点,所以OM为△NFF'的中位线,
所以OM∥PF'
因为|OM|=a,所以|NF'|=2a
又NF'⊥NF,|FF'|=2c 所以|NF|=2b
设N(x,y),则由抛物线的定义可得x+c=2a,
∴x=2a-c
过点F作x轴的垂线,点N到该垂线的距离为2a
由勾股定理 y2+4a2=4b2,即4c(2a-c)+4a2=4(c2-a2)
得e2-e-1=0,
∴e=
| ||
| 2 |
故选:D.
点评:本题主要考查双曲线的标准方程,以及双曲线的简单性质的应用,考查抛物线的定义,考查运算求解能力,考查数形结合思想、化归与转化思想,属于中档题.

练习册系列答案
相关题目
若幂函数f(x)=mxα的图象经过点A(
,
),则它在点A处的切线方程是( )
| 1 |
| 4 |
| 1 |
| 2 |
| A、2x-y=0 |
| B、2x+y=0 |
| C、4x-4y+1=0 |
| D、4x+4y+1=0 |
已知f(x)=
,不等式f(x+a)>f(2a-x)在[a,a+1]上恒成立,则实数a的取值范围是( )
|
| A、(-∞,-2) |
| B、(-∞,0) |
| C、(0,2) |
| D、(-2,0) |
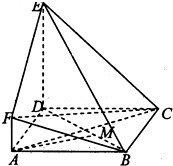 如图,ABCD是正方形,DE⊥平面ABCD.
如图,ABCD是正方形,DE⊥平面ABCD.