题目内容
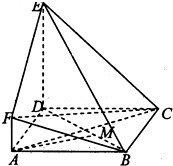如图，ABCD是正方形，DE⊥平面ABCD．（1）求证：AC⊥平面BDE；
（2）若AF∥DE，DE=3AF，点M在线段BD上，且BM=
| 1 |
| 3 |
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）证明DE⊥AC，通过直线与平面垂直的判定定理证明AC⊥平面BDE．
（2）延长EF、DA交于点G，通过AF∥DE，DE=3AF，推出
=
=
，证明AM∥GB利用直线与平面平行的判定定理证明AM∥平面BEF．
（2）延长EF、DA交于点G，通过AF∥DE，DE=3AF，推出
| BM |
| BD |
| GA |
| GD |
| 1 |
| 3 |
解答：
证明：
（1）因为DE⊥平面ABCD，所以DE⊥AC．…（2分）
因为ABCD是正方形，所以AC⊥BD，又BD∩DE=D，
从而AC⊥平面BDE．…（5分）
（2）延长EF、DA交于点G，
因为AF∥DE，DE=3AF，
所以
=
=
，…（7分）
因为BM=
BD，所以
=
，
所以
=
=
，所以AM∥GB，…（10分）
又AM?平面BEF，GB?平面BEF，
所以AM∥平面BEF．…（12分）
（1）因为DE⊥平面ABCD，所以DE⊥AC．…（2分）因为ABCD是正方形，所以AC⊥BD，又BD∩DE=D，
从而AC⊥平面BDE．…（5分）
（2）延长EF、DA交于点G，
因为AF∥DE，DE=3AF，
所以
| GA |
| GD |
| AF |
| DE |
| 1 |
| 3 |
因为BM=
| 1 |
| 3 |
| BM |
| BD |
| 1 |
| 3 |
所以
| BM |
| BD |
| GA |
| GD |
| 1 |
| 3 |
又AM?平面BEF，GB?平面BEF，
所以AM∥平面BEF．…（12分）
点评：本题考查直线与平面垂直的判定定理以及直线与平面平行的判定定理的应用，考查空间想象能力以及逻辑推理能力．
练习册系列答案
名校课堂系列答案
相关题目
已知数列{an}满足anan-1=an-1+（-1）n且a1=1，则
=（ ）
| a5 |
| a3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
过曲线C1：
-
=1（a＞0，b＞0）的左焦点F作曲线C2：x2+y2=a2的切线，设切点为M，延长FM交曲线C3：y2=2px（p＞0）于点N，其中曲线C1与C3有一个共同的焦点，若点M为线段FN的中点，则曲线C1的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从抛物线y2=16x上一点P引抛物线准线的垂线，垂足为M，设抛物线的焦点为F，|PF|=8，则△MPF的面积是 （ ）
| A、20 | B、25 | C、28 | D、32 |
sin3的取值所在的范围是（ ）
A、（
| ||||
B、（0，
| ||||
C、（-
| ||||
D、（-1，-
|
在极坐标系中，圆ρ=2cosθ的半径为（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
已知实数x，y满足不等式组
，若目标函数z=y-ax去的最大值时的唯一最优解为（1，3），则实数a的取值范围为（ ）
|
| A、（1，+∞） |
| B、[1，+∞） |
| C、（0，1） |
| D、（-∞，-1） |