题目内容
等差数列{an}中,a7=-11,a2=4a3
(1)求{an}的通项公式;
(2)求|a1|+|a2|+…+|an|.
(1)求{an}的通项公式;
(2)求|a1|+|a2|+…+|an|.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式列出方程组,求出首项和公差,由此能求出an=-3n+10.
(2)由a1=7,d=-3,得等差数列{an}的前n项和Sn=-
n2+
n,由an=-3n+10≥0,得n≤
,从而1≤n≤3时,an>0,n≥4时,an<0.设|a1|+|a2|+…+|an|=Tn,当1≤n≤3时,Tn=Sn,当n≥4时,Tn=2S3-Sn,由此能求出|a1|+|a2|+…+|an|.
(2)由a1=7,d=-3,得等差数列{an}的前n项和Sn=-
| 3 |
| 2 |
| 17 |
| 2 |
| 10 |
| 3 |
解答:
解:(1)∵等差数列{an}中,a7=-11,a2=4a3,
∴
,
解得a1=7,d=-3,
∴an=7+(n-1)×(-3)=-3n+10.
(2)∵a1=7,d=-3,
∴等差数列{an}的前n项和Sn=7n+
×(-3)=-
n2+
n,
由an=-3n+10≥0,得n≤
,
∴1≤n≤3时,an>0,n≥4时,an<0.
设|a1|+|a2|+…+|an|=Tn,
∴当1≤n≤3时,Tn=Sn=-
n2+
n,
当n≥4时,Tn=2S3-Sn=
n2-
n+24.
∴|a1|+|a2|+…+|an|=
.
∴
|
解得a1=7,d=-3,
∴an=7+(n-1)×(-3)=-3n+10.
(2)∵a1=7,d=-3,
∴等差数列{an}的前n项和Sn=7n+
| n(n-1) |
| 2 |
| 3 |
| 2 |
| 17 |
| 2 |
由an=-3n+10≥0,得n≤
| 10 |
| 3 |
∴1≤n≤3时,an>0,n≥4时,an<0.
设|a1|+|a2|+…+|an|=Tn,
∴当1≤n≤3时,Tn=Sn=-
| 3 |
| 2 |
| 17 |
| 2 |
当n≥4时,Tn=2S3-Sn=
| 3 |
| 2 |
| 17 |
| 2 |
∴|a1|+|a2|+…+|an|=
|
点评:本题考查数列的通项公式和前n项和的求法,是中档题,解题时要认真审题,注意等差数列的性质和分类讨论思想的合理运用.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
已知|
|=1,|
|=2,
•(
-
)=-2,则向量
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知变量x与y负相关,且由观测数据算得样本平均数
=4,
=4.5,则由该观测数据算得的线性回归方程可能是( )
. |
| x |
. |
| y |
A、
| ||
B、
| ||
C、
| ||
D、
|
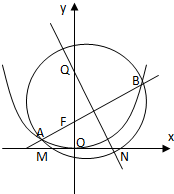 已知抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5).
已知抛物线C:x2=2py(p>0)的焦点为F,过F的直线l交抛物线C于点A,B,当直线l的倾斜角是45°时,AB的中垂线交y轴于点Q(0,5).
