题目内容
已知曲线C1的参数方程是
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程是ρ=-4cosθ.
(1)求曲线C1与C2交点的极坐标;
(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).
|
(1)求曲线C1与C2交点的极坐标;
(2)A、B两点分别在曲线C1与C2上,当|AB|最大时,求△OAB的面积(O为坐标原点).
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)把
消去θ化为普通方程,由极坐标方程ρ=-4cosθ化为直角坐标方程得x2+y2=-4x,联立求出交点的直角坐标,化为极坐标得答案;
(2)画出两圆,数形结合得到A,C1,C2,B依次排列且共线时|AB|最大,求出|AB|及O到AB的距离代入三角形的面积公式得答案.
|
(2)画出两圆,数形结合得到A,C1,C2,B依次排列且共线时|AB|最大,求出|AB|及O到AB的距离代入三角形的面积公式得答案.
解答:
解:(1)由
,得
,两式平方作和得:x2+(y-2)2=4,即x2+y2-4y=0;
由ρ=-4cosθ,得ρ2=-4ρcosθ,即x2+y2=-4x.
两式作差得:x+y=0,代入C1得交点为(0,0),(-2,2).
其极坐标为(0,0),(2
,
);
(2)如图,
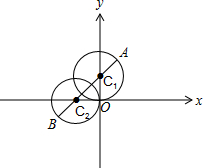
由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.
此时|AB|=2
+4,O到AB的距离为
.
∴△OAB的面积为S=
×(2
+4)×
=2+2
.
|
|
由ρ=-4cosθ,得ρ2=-4ρcosθ,即x2+y2=-4x.
两式作差得:x+y=0,代入C1得交点为(0,0),(-2,2).
其极坐标为(0,0),(2
| 2 |
| 3π |
| 4 |
(2)如图,

由平面几何知识可知,A,C1,C2,B依次排列且共线时|AB|最大.
此时|AB|=2
| 2 |
| 2 |
∴△OAB的面积为S=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了参数方程化普通方程,极坐标与直角坐标的互化,考查了数形结合的解题思想方法,是基础的计算题.

练习册系列答案
相关题目
过曲线C1:
-
=1(a>0,b>0)的左焦点F作曲线C2:x2+y2=a2的切线,设切点为M,延长FM交曲线C3:y2=2px(p>0)于点N,其中曲线C1与C3有一个共同的焦点,若点M为线段FN的中点,则曲线C1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin3的取值所在的范围是( )
A、(
| ||||
B、(0,
| ||||
C、(-
| ||||
D、(-1,-
|
在极坐标系中,圆ρ=2cosθ的半径为( )
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |
已知实数x,y满足不等式组
,若目标函数z=y-ax去的最大值时的唯一最优解为(1,3),则实数a的取值范围为( )
|
| A、(1,+∞) |
| B、[1,+∞) |
| C、(0,1) |
| D、(-∞,-1) |
定义符号函数sgn(x)=
,则下列结论中错误的是( )
|
| A、x=sgn(x)•|x| | ||
B、sgn(x)=
| ||
| C、sgn(x•y)=sgn(x)•sgn(y) | ||
| D、sgn(x+y)=sgn(x)+sgn(y) |
