题目内容
16. 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.(Ⅰ)求证:CE∥平面PAD;
(Ⅱ)求直线CE与平面PAC所成角的正切值.
分析 (1)取PA中点Q,连结QE、QD,推导出四边形QECD是平行四边形,由此能证明CE∥平面PAD.
(2)过E作平面PAC的垂线,记垂足为O,连结CO,∠ECO是直线CE与平面PAC所成的角,过B作BN⊥AC,记垂足为N,过E作EM⊥AB=M,连结CM,由此能求出直线CE与平面PAC所成角的正切值.
解答  证明:(1)取PA中点Q,连结QE、QD,
证明:(1)取PA中点Q,连结QE、QD,
∵E为PB中点,∴QE∥AB,且QE=$\frac{1}{2}$AB,
∵底面ABCD是直角梯形,∠CDA=∠BDA=90°,AB=AD=2DC=2$\sqrt{2}$,
∴QE∥CD,且QE=CD,∴四边形QECD是平行四边形,
∴EC∥QD,又EC?平面PAD,QD?平面PAD,
∴CE∥平面PAD.
解:(2)过E作平面PAC的垂线,记垂足为O,连结CO,
则∠ECO是直线CE与平面PAC所成的角,
过B作BN⊥AC,记垂足为N,
∵PA⊥平面ABCD,∴PA⊥BN,
又PA,AC?平面PAC,且PA∩AC=A,
∴BN⊥平面PAC,
∴EO∥BN,又∵E是AB的中点,∴EO=$\frac{1}{2}$BN=$\frac{2\sqrt{10}}{5}$,
过E作EM⊥AB=M,连结CM,得CE=2$\sqrt{3}$,
在Rt△CEO中,CO=$2\sqrt{\frac{13}{5}}$,则tan∠ECO=$\frac{EO}{CO}$=$\frac{\sqrt{26}}{13}$,
∴直线CE与平面PAC所成角的正切值为$\frac{\sqrt{26}}{13}$.
点评 本题考查线面平行的证明,考查线面角的正切值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.下列命题中正确的个数是
①若¬p是q的必要而不充分条件,则p是¬q的充分而不必要条件;
②命题“对任x∈R,都x2≥0”的否定为“存x0∈R,使x02<0”;
③若p∧q为假命题,则p与q均为假命题.( )
①若¬p是q的必要而不充分条件,则p是¬q的充分而不必要条件;
②命题“对任x∈R,都x2≥0”的否定为“存x0∈R,使x02<0”;
③若p∧q为假命题,则p与q均为假命题.( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
8.总体由编号为00,01,02,…,19的20个个体组成,利用下面给出的随机数表从20个个体中选取5个个体,选取方法是从随机数表第一行的第5列数字开始由左到右依次选定两个数字,则选出来的第5个个体编号为( )
| 78 | 16 | 95 | 72 | 08 | 14 | 07 | 43 | 63 | 42 | 03 | 20 | 97 | 28 | 01 | 98 |
| 32 | 04 | 92 | 34 | 49 | 35 | 82 | 40 | 36 | 23 | 48 | 69 | 69 | 38 | 74 | 81 |
| A. | 01 | B. | 07 | C. | 08 | D. | 20 |
5.(重点中学做)“x<-1”是“ln(x+2)<0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.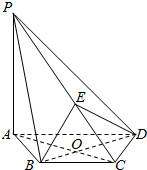 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE, 某几何体的三视图如图所示,其俯视图的外轮廓是由一个半圆与其直径组成的图形,则此几何体的体积是$\frac{8π}{3}$.
某几何体的三视图如图所示,其俯视图的外轮廓是由一个半圆与其直径组成的图形,则此几何体的体积是$\frac{8π}{3}$.