题目内容
11.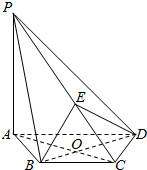 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥BD于O,E为线段PC上一点,且AC⊥BE,(1)求证:PA∥平面BED;
(2)若BC∥AD,BC=$\sqrt{2}$,AD=2$\sqrt{2}$,PA=3且AB=CD,求PB与面PCD所成角的正弦值.
分析 (1)连接OE,推导出AC⊥OE,AC⊥PA,从而OE∥PA,由此能证明PA∥平面BED.
(2)分别以OB,OC,OE为x,y,z轴建立空间直角坐标系O-xyz,利用向量法能求出PB与平面PCD所成角的正弦值.
解答  (本小题满分12分)
(本小题满分12分)
证明:(1)∵AC⊥BD,AC⊥BE,BD∩BE=B,
∴AC⊥平面BDE,连接OE,…(1分)
∴AC⊥OE,又PA⊥平面ABCD,
∴AC⊥PA,又OE,PA都是平面PAC中的直线,
∴OE∥PA,…(3分)
∵OE?平面BDE,PA?平面BDE,
∴PA∥平面BED.…(4分)
解:(2)∵BC∥AD,BC=$\sqrt{2}$,AD=2$\sqrt{2}$,且AB=CD,
∴在等腰梯形ABCD中,OB=OC=1,OA=OD=2,…(5分)
由(1)知OE⊥平面ABCD,分别以OB,OC,OE为x,y,z轴建立空间直角坐标系O-xyz,
则B(1,0,0),C(0,1,0),D(-2,0,0),P(0,-2,3),…(6分)
设平面PCD的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{CD}=-2x-y=0}\\{\overrightarrow{n}•\overrightarrow{PC}=3y-3z=0}\end{array}\right.$,
取x=1,则y=z-2,$\overrightarrow{n}$=(1,-2,-2),…(9分)
又$\overrightarrow{PB}$=(1,2,-3),
∴cos<$\overrightarrow{PB},\overrightarrow{n}$>=$\frac{\overrightarrow{PB}•\overrightarrow{n}}{|\overrightarrow{PB}|•|\overrightarrow{n}|}$=$\frac{\sqrt{14}}{14}$,…(11分)
∴PB与平面PCD所成角的正弦值为$\frac{\sqrt{14}}{14}$.…(12分)
点评 本题考查线面平行的证明,考查线面角的正弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

| A. | [$\frac{2}{3}$,2] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [1,2] |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $\frac{1}{4}<m<1$ | B. | m>1 | C. | $m<\frac{1}{4}$ | D. | $m<\frac{1}{4}$或m>1 |
 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为直角梯形,∠CDA=∠BAD=90°,AB=AD=2DC=2$\sqrt{2}$,PA=4且E为PB的中点.