题目内容
18.若函数f(x)=x3-ax2-x+6在(0,1)上单调递减,则实数a取值范围是( )| A. | a=1 | B. | a≥1 | C. | a≤1 | D. | 0<a<1 |
分析 若函数f(x)=x3-ax2-x+6在(0,1)上单调递减,则f′(x)=3x2-2ax-1≤0,在(0,1)上恒成立,即a≥$\frac{3{x}^{2}-1}{2x}$在(0,1)上恒成立,进而得到答案.
解答 解:∵函数f(x)=x3-ax2-x+6,
∴f′(x)=3x2-2ax-1,
∵函数f(x)=x3-ax2-x+6在(0,1)上单调递减,
∴f′(x)=3x2-2ax-1≤0,在(0,1)上恒成立,
即a≥$\frac{3{x}^{2}-1}{2x}$在(0,1)上恒成立,
令g(x)=$\frac{3{x}^{2}-1}{2x}$,则g′(x)=$\frac{3{x}^{2}+1}{2{x}^{2}}$>0在(0,1)上恒成立,
故g(x)=$\frac{3{x}^{2}-1}{2x}$在(0,1)上为增函数,
由g(1)=1得:a≥1,
故选:B.
点评 本题考查的知识点是利用导数研究函数的单调性,函数恒成立问题,难度中档.

练习册系列答案
相关题目
8.函数f(x)的图象如图所示,则f(x)的解析式是( )
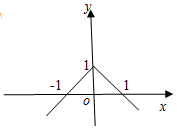

| A. | f(x)=-|x|-1 | B. | f(x)=|x-1| | C. | f(x)=-|x|+1 | D. | f(x)=|x+1| |
7.空间二直线a,b和二平面α,β,下列一定成立的命题是( )
| A. | 若α⊥β,a⊥b,a⊥α,则b⊥β | B. | 若α⊥β,a⊥b,a⊥α,则b∥β | ||
| C. | 若α⊥β,a∥α,b∥β,则a⊥b | D. | 若α∥β,a⊥α,b?β,则a⊥b |