题目内容
6.若函数y=f(x)(x∈R)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=1-x2.函数$g(x)=\left\{\begin{array}{l}lgx,x>0\\|\frac{1}{2}x+2|,x≤0\end{array}\right.$,则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 已知函数偶函数f(x)满足f(x+2)=f(x),可知f(x)周期为2,且x∈[-1,1]时,f(x)=1-x2,根据偶函数的性质画出f(x)的图象,根据分段函数$g(x)=\left\{\begin{array}{l}lgx,x>0\\|\frac{1}{2}x+2|,x≤0\end{array}\right.$,画出g(x)的图象,利用数形结合的方法求出函数h(x)=f(x)-g(x)在区间[-5,5]内的零点个数
解答 解:在R上的函数偶函数f(x)满足f(x+2)=f(x),可知f(x)周期为2,
x∈[-1,1]时,f(x)=1-x2,
故函数f(x)的图象如下图所示:
函数$g(x)=\left\{\begin{array}{l}lgx,x>0\\|\frac{1}{2}x+2|,x≤0\end{array}\right.$的图象如下图所示:
函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数,即为f(x)=g(x)时的交点,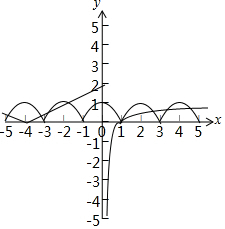
由上图可知f(x)与g(x)有8个交点,
∴h(x)在区间[-5,5]内的零点的个数为8个,
故选:C
点评 此题主要考查偶函数的性质,以及零点定理的应用,解题的过程中用到了数形结合的方法,这也是高考常考的热点问题,此题是一道中档题.

练习册系列答案
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
18.若函数f(x)=x3-ax2-x+6在(0,1)上单调递减,则实数a取值范围是( )
| A. | a=1 | B. | a≥1 | C. | a≤1 | D. | 0<a<1 |
15.若$\frac{cos2α}{sinα-cosα}$=-$\frac{1}{2}$,则sin(α+$\frac{π}{4}$)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{2}}{4}$ |
 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.
在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.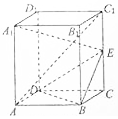 在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证:
在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证: