Question

8．函数f（x）的图象如图所示，则f（x）的解析式是（　　）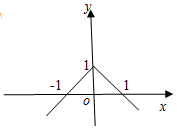

• A． f（x）=-|x|-1
• B． f（x）=|x-1|
• C． f（x）=-|x|+1
• D． f（x）=|x+1|

Answer 1

分析 根据图象可知，函数f（x）的图象是由两条直线构成，设出f（x），利用坐标求解即可．

解答 解：根据图象可知，函数f（x）的图象是由两条直线构成，
设f（x）=kx+b，
当x≥0时，图象过（0，1）和（1，0）．
可得f（x）=-x+1，
当x＜0时，图象过（0，1）和（-1，0）．
可得f（x）=x+1，
∴可得f（x）在R上的解析式为f（x）=-|x|+1．
故选C．

点评 本题考查了通过图象求解函数解析式的问题．比较基础题．