题目内容
8.△ABC的周长等于3(sinA+sinB+sinC),则其外接圆直径等于3.分析 由正弦定理和△ABC的外接圆半径表示出sinA、sinB、sinC,代入已知的式子化简后求出答案.
解答 解:由正弦定理得,$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,
且R是△ABC的外接圆半径,
则sinA=$\frac{a}{2R}$,sinB=$\frac{b}{2R}$,sinC=$\frac{c}{2R}$,
因为△ABC的周长等于3(sinA+sinB+sinC),
所以a+b+c=3(sinA+sinB+sinC)=3($\frac{a}{2R}$+$\frac{b}{2R}$+$\frac{c}{2R}$),
化简得,2R=3,
即其外接圆直径等于3,
故答案为:3.
点评 本题考查了正弦定理的应用:边角互化,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.若函数f(x)=x3-ax2-x+6在(0,1)上单调递减,则实数a取值范围是( )
| A. | a=1 | B. | a≥1 | C. | a≤1 | D. | 0<a<1 |
3.已知lg(x+y)=lgx+lgy,则x+y的取值范围是( )
| A. | (0,1] | B. | [2,+∞) | C. | (0,4] | D. | [4,+∞) |
13.执行如图所示的程序框图,输出的S值为( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
17.函数$y=sin(ωx+\frac{π}{6})(ω>0)$的图象与x轴正半轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,若要得到函数g(x)=sinωx的图象,只要将f(x)的图象( )个单位.
| A. | 向左平移$\frac{π}{12}$ | B. | 向右平移$\frac{π}{12}$ | C. | 向左平移$\frac{π}{6}$ | D. | 向右平移$\frac{π}{6}$ |
18.设集合A={x|2x≤8},B={x|x≤m2+m+1},若A∪B=A,则实数m的取值范围为.( )
| A. | [-2,1) | B. | [-2,1] | C. | [-2,-1) | D. | [-1,1) |
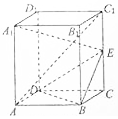 在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证:
在长方体ABCD-A1B1C1D1中,AB=BC=EC=$\frac{1}{2}A{A}_{1}$.求证: