题目内容
10.已知函数f(x)=xk,x∈R,k为常数.(Ⅰ)当k=3时,判断函数f(x)的奇偶性,并说明理由;
(Ⅱ)当k=1时,设函数g(x)=f(x)+$\frac{4}{f(x)}$,判断函数g(x)在区间(0,2]上的单调性,利用函数单调性的定义证明你的结论.
分析 (Ⅰ)根据函数奇偶性的定义进行判断;
(Ⅱ)求出函数g(x)的表达式,结合函数单调性的定义进行判断.
解答 解:(Ⅰ)当k=3时,f(x)=x3,则f(-x)=(-x)3=-x3=-f(x),
则函数f(x)为奇函数;
(Ⅱ)当k=1时,函数g(x)=f(x)+$\frac{4}{f(x)}$=x+$\frac{4}{x}$,
则函数在间(0,2]上的单调递减,
证明:0<x1<x2≤2,
则$f({x_1})-f({x_2})={x_1}+\frac{4}{x_1}-{x_2}-\frac{4}{x_2}=({x_1}-{x_2})+\frac{{4({x_2}-{x_1})}}{{{x_1}{x_2}}}=({x_1}-{x_2})(1-\frac{4}{{{x_1}{x_2}}})$=(x1-x2)•$\frac{{x}_{1}{x}_{2}-4}{{x}_{1}{x}_{2}}$,
∵0<x1<x2≤2,
∴x1-x2<0,0<x1x2<4,
∴f(x1)-f(x2)>0,
∴函数g(x)在区间(0,2]上的单调递减.
点评 本题主要考查函数奇偶性和单调性的判断和应用,结合函数奇偶性和单调性的定义是解决本题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
18.若函数f(x)=x3-ax2-x+6在(0,1)上单调递减,则实数a取值范围是( )
| A. | a=1 | B. | a≥1 | C. | a≤1 | D. | 0<a<1 |
5.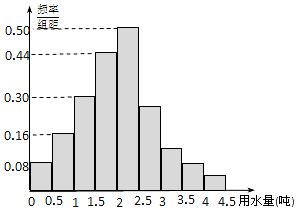 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
(1)根据频率分布直方图估计这组数据的众数与平均数;
(2)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?
 某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:
某地区100位居民的人均月用水量(单位:t)的频率分布直方图及频数分布表如下:| 分组 | 频数 |
| [0,0.5) | 4 |
| [0.5,1) | 8 |
| [1,1.5) | 15 |
| [1.5,2) | 22 |
| [2,2.5) | 25 |
| [2.5,3) | 14 |
| [3,3.5) | 6 |
| [3.5,4) | 4 |
| [4,4.5) | 2 |
| 合计 | 100 |
(2)当地政府制定了人均月用水量为3t的标准,若超出标准加倍收费,当地政府解释说,85%以上的居民不超出这个标准,这个解释对吗?为什么?
15.若$\frac{cos2α}{sinα-cosα}$=-$\frac{1}{2}$,则sin(α+$\frac{π}{4}$)的值为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | -$\frac{\sqrt{2}}{4}$ |
2.函数f(x)=$\frac{ln(4-x)}{x-2}$的定义域是( )
| A. | (-∞,4) | B. | (2,4) | C. | (0,2)∪(2,4) | D. | (-∞,2)∪(2,4) |
 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.
在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.