题目内容
已知数列{an},{bn}各项均为正数,且对任意n∈N*,都有an,bn,a n+1成等差数列,bn,a n+1,b n+1成等比数列,且a1=10,a2=15,求证:{
}为等差数列并求出{an},{bn}的通项公式.
| bn |
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:由已知得an+12=bn•bn+1,(n∈N*),从而an=
,(n≥2),由an,bn,an+1成等差数列,得2
=
+
,(n≥2),由此能证明数列{
}是等差数列.由a1=10,a2=15,得
=
,从而bn=(2
+
)2=
+4n+8,(n≥2),由此能求出bn=
+4n+8,(n∈N*),an=
n2+
n+6.(n∈N*).
| bnbn-1 |
| bn |
| bn-1 |
| bn+1 |
| bn |
| b1 |
5
| ||
| 2 |
| 2 |
| ||
| 2 |
| n2 |
| 2 |
| n2 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
解答:
证明:∵bn,a n+1,b n+1成等比数列,
∴an+12=bn•bn+1,(n∈N*)
∴an+1=
,
∴an=
,(n≥2)
∵an,bn,an+1成等差数列,
∴2bn=an+an+1,(n∈N*)
∴2bn=
+
=
(
+
),(n≥2)
2
=
+
,(n≥2)
∴数列{
}是等差数列.
∵a1=10,a2=15,∴2b1=a1+a2=25,b1=
,
=
,
∵an=
,(n≥2),
∴a2=
,
=
=3
,
∴d=
-
=
,∴
=
+(n-1)•
=2
+
n,
∴bn=(2
+
)2=
+4n+8,(n≥2)
当n=1时,解得b1=
,∴bn=
+4n+8,(n∈N*)
an=
bn-1=
=(2
+
)(2
+
)
=8+2n+2(n-1)+
n(n-1)
=
n2+
n+6.(n≥2)
当n=1时,解得a1=10,满足条件,
∴an=
n2+
n+6.(n∈N*)
∴an+12=bn•bn+1,(n∈N*)
∴an+1=
| bnbn+1 |
∴an=
| bnbn-1 |
∵an,bn,an+1成等差数列,
∴2bn=an+an+1,(n∈N*)
∴2bn=
| bn×bn-1 |
| bn×bn+1 |
| bn |
| bn-1 |
| bn+1 |
2
| bn |
| bn-1 |
| bn+1 |
∴数列{
| bn |
∵a1=10,a2=15,∴2b1=a1+a2=25,b1=
| 25 |
| 2 |
| b1 |
5
| ||
| 2 |
∵an=
| bn-1bn |
∴a2=
| b1 |
| b2 |
| b2 |
| a2 | ||
|
| 2 |
∴d=
| b2 |
| b1 |
| ||
| 2 |
| bn |
5
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
∴bn=(2
| 2 |
| ||
| 2 |
| n2 |
| 2 |
当n=1时,解得b1=
| 25 |
| 2 |
| n2 |
| 2 |
an=
| bn |
(2
|
=(2
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
=8+2n+2(n-1)+
| 1 |
| 2 |
=
| 1 |
| 2 |
| 7 |
| 2 |
当n=1时,解得a1=10,满足条件,
∴an=
| 1 |
| 2 |
| 7 |
| 2 |
点评:本题考查等差数列的证明,考查数列的通项公式的求法,是中档题,解题时要认真审题,注意构造法的合理运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
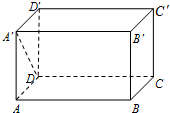 如图,在长方体ABCD-A′B′C′D′中,AB=6,AA′=BC=4,则A′D与BC所成的角等于( )
如图,在长方体ABCD-A′B′C′D′中,AB=6,AA′=BC=4,则A′D与BC所成的角等于( )| A、30° | B、45° |
| C、60° | D、90° |
 一个圆柱形容器里装有水,放在水平面上,现将容器倾斜,这时水面是一个椭圆,当圆柱的母线AB与地面所成角
一个圆柱形容器里装有水,放在水平面上,现将容器倾斜,这时水面是一个椭圆,当圆柱的母线AB与地面所成角