题目内容
已知向量
=(
sin
,a),
=(acos
,cos2
)且a>0,f(x)=
•
.函数f(x)的图象过最大值点(x0,3)及相邻的最小值点(x0+π,-1).
(1)求f(x)的解析式;
(2)若α∈(-
,
)且f(α)=
,求
的值.
| m |
| 3 |
| ωx |
| 2 |
| n |
| ωx |
| 2 |
| ωx |
| 2 |
| m |
| n |
(1)求f(x)的解析式;
(2)若α∈(-
| π |
| 2 |
| π |
| 2 |
| 3 |
| 2 |
cos(α+
| ||
| sinα |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:三角函数的图像与性质
分析:(1)化简可得f(x)=asin(ωx+
)+
,由图象特点可得a=2,ω=1,可得解析式;
(2)可得sin(α+
)=
,由范围和同角三角函数基本关系可得cos(α+
),进而可得sinα,代入计算可得.
| π |
| 6 |
| a |
| 2 |
(2)可得sin(α+
| π |
| 6 |
| 1 |
| 4 |
| π |
| 6 |
解答:
解:(1)∵
=(
sin
,a),
=(acos
,cos2
)且a>0,
∴f(x)=
•
=
asin
cos
+acos2
=
asinωx+a
=asin(ωx+
)+
,
又∵f(x)的图象过最大值点(x0,3)及最小值点(x0+π,-1),
∴a=2,
=π,即ω=1
∴f(x)=2sin(x+
)+1
(2)∵f(α)=
,∴sin(α+
)=
,
又∵α∈(-
,
)且sin(α+
)=
<
,
∴0<α+
<
,
∴cos(α+
)=
=
∴sinα=sin[(α+
)-
]=
∴
=
=-
| m |
| 3 |
| ωx |
| 2 |
| n |
| ωx |
| 2 |
| ωx |
| 2 |
∴f(x)=
| m |
| n |
| 3 |
| ωx |
| 2 |
| ωx |
| 2 |
| ωx |
| 2 |
=
| ||
| 2 |
| 1+cos2ωx |
| 2 |
| π |
| 6 |
| a |
| 2 |
又∵f(x)的图象过最大值点(x0,3)及最小值点(x0+π,-1),
∴a=2,
| π |
| ω |
∴f(x)=2sin(x+
| π |
| 6 |
(2)∵f(α)=
| 3 |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
又∵α∈(-
| π |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 4 |
| ||
| 2 |
∴0<α+
| π |
| 6 |
| π |
| 4 |
∴cos(α+
| π |
| 6 |
1-sin2(α+
|
| ||
| 4 |
∴sinα=sin[(α+
| π |
| 6 |
| π |
| 6 |
| ||||
| 8 |
∴
cos(α+
| ||
| sinα |
| ||||||
|
5+
| ||
| 2 |
点评:本题考查三角函数的运算,涉及向量数量积和同角三角函数的基本关系,属中档题.

练习册系列答案
相关题目
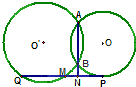 如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.
如图,⊙O′和⊙O相交于A和B,PQ切⊙O于P,交⊙O′于Q和M,交AB的延长线于N,MN=3,NQ=15,求PN的长.