题目内容
设等差数列{an}的前n项和为Sn,首项a1>0,S12>0,S13<0.则以下关于数列{an}的判断中正确的个数有
( )
①a6a7>0;
②|a6|>|a7|;
③a5+a8>0;
④前n项和Sn中最大的项为第六项.
( )
①a6a7>0;
②|a6|>|a7|;
③a5+a8>0;
④前n项和Sn中最大的项为第六项.
| A、1 | B、2 | C、3 | D、4 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:根据所给的等差数列的S12>0,S13<0,根据等差数列的前n项和公式,看出第七项小于0,第六项和第七项的和大于0,得到第六项大于0,这样前6项的和最大.
解答:
解:∵等差数列{an}中,S12>0,且S13<0,
即S12=6(a6+a7)>0,S13=13a7<0,
∴a6+a7>0,a7<0,
∴a6>0,a7<0,
∵a6a7<0,|a6|>|a7|,
a5+a8=a5+a8>0,
∵d<0,
∴Sn达到最大值时对应的项数n的值为6.
∴②③④正确.
故选:C.
即S12=6(a6+a7)>0,S13=13a7<0,
∴a6+a7>0,a7<0,
∴a6>0,a7<0,
∵a6a7<0,|a6|>|a7|,
a5+a8=a5+a8>0,
∵d<0,
∴Sn达到最大值时对应的项数n的值为6.
∴②③④正确.
故选:C.
点评:本题考查等差数列的性质和前n项和,本题解题的关键是看出所给的数列的项的正负,本题是一个基础题.

练习册系列答案
相关题目
已知数列{an}满足a1=2,an+1=
,则a2014等于( )
| 1+an |
| 1-an |
| A、2 | ||
B、-
| ||
| C、-3 | ||
D、
|
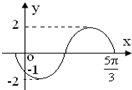 已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为( )
已知函数f(x)=2sin(ωx+φ)(ω>0,-π<φ<π)图象的一部分(如图所示),则ω与φ的值分别为( )A、
| ||||
B、1,-
| ||||
C、
| ||||
D、
|
等比数列{an}中,a1=2,a8=4,函数f(x)=x(x-a4)(x-a5),则[f′(0)]4=( )
| A、216 |
| B、212 |
| C、28 |
| D、24 |
椭圆
+y2=1的焦距比短轴长( )
| x2 |
| 10 |
A、
| ||
B、2
| ||
| C、2 | ||
| D、4 |
等差数列的相邻4项分别是a+1,a+3,b,a+b,那么a,b的值依次为( )
| A、2,7 | B、1,6 |
| C、0,5 | D、无法确定 |
已知f(x)=ln(
-3x)+1,则f(lg3)+f(lg
)等于( )
| 1+9x2 |
| 1 |
| 3 |
| A、2 | B、1 | C、0 | D、-1 |
已知等比数列{an},若a1+a2=20,a3+a4=80,则a5+a6等于( )
| A、480 | B、120 |
| C、240 | D、320 |