Question

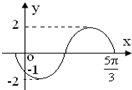已知函数f（x）=2sin（ωx+φ）（ω＞0，-π＜φ＜π）图象的一部分（如图所示），则ω与φ的值分别为（　　）

• A、

  11

  10

  ，-

  5π

  6

• B、1，-

  2π

  3

• C、

  7

  10

  ，-

  π

  6

• D、

  4

  5

  ，-

  π

  3

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由f（0）=-1，-π＜φ＜π，可求得φ=-

π

6

或φ=-

5π

6

；利用T=

2π

ω

＞

5π

3

，且

3

4

T＜

5π

3

，可求得ω∈（

9

10

，

6

5

）；分φ=-

π

6

与φ=-

5π

6

讨论，即可求得答案．

解答： 解：∵f（0）=2sinφ=-1，
∴sinφ=-

1

2

，又-π＜φ＜π，
∴φ=-

π

6

或φ=-

5π

6

；
由图知，T=

2π

ω

＞

5π

3

，且

3

4

T=

3

4

×

2π

ω

＜

5π

3

，
∴

9

10

＜ω＜

6

5

；
又

5π

3

ω+φ=π，
∴当φ=-

π

6

时，

5π

3

ω+φ=π，解得ω=

7

10

∉（

9

10

，

6

5

），舍去；
当φ=-

5π

6

时，由

5π

3

ω-

5π

6

=π，得ω=

11

10

∈（

9

10

，

6

5

）．
∴ω与φ的值分别为：

11

10

，-

5π

6

．
故选：A．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，考查识图与运算求解、等价转化思想与分类讨论思想的综合应用，属于中档题．