题目内容
3．
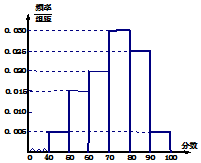某校从高三年级期末考试的学生中抽出20名学生，其成绩（均为整数）的频率分布直方图如图所示：（1）估计这次考试的及格率（60分及以上为及格）和平均分；
（2）从成绩是80分以上（包括80分）的学生中选两人，求他们在不同分数段的概率．
分析 （1）求出60分及以上的频率为及格率，再利用组中值计算平均分；
（2）求出80到90分以及90到100分的人数，利用列举法求出对应的基本事件数，计算概率值即可．
解答 解：（1）60分及以上的频率为1-（0.005+0.015）×10=0.8，
所以及格率为0.8；
平均分为：45×0.05+55×0.15+65×0.2+75×0.30+85×0.25+95×0.05=72；
（2）80到90分的人数为：0.025×10×20=5（人），
90到100分人数为：0.005×10×20=1（人）；
设90到100分的人为a，80到90分的5个人分别为：1、2、3、4、5，
则有（a，1）、（a，2）、（a，3）、（a，4）、（a，5）、
（1，2）、（1，3）、（1，4）、（1，5）、
（2，3）、（2，4）、（2，5）、
（3，4）、（3，5）、（4，5）共15个基本事件，且他们是等可能的，
设事件A为选中的两人在不同分数段，则事件A有
（a，1）、（a，2）、（a，3）、（a，4），（a，5）共5个基本事件，
∴P（A）=$\frac{5}{15}$=$\frac{1}{3}$．
即成绩是80分以上（包括80分）的学生中选两人，在不同分数段的概率为$\frac{1}{3}$．
点评 本题考主要查古典概型问题，可以列举出试验发生包含的事件和满足条件的事件，列举法，是解决古典概型问题的一种重要的解题方法，属于基础题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
13．下面函数中在定义域内是奇函数和单调增函数的是（ ）
| A． | y=e-x-ex | B． | y=tanx | C． | y=x-3|x| | D． | y=ln（x+2）-ln（2-x） |
14．某公司的广告费支出x与销售额y（单位：万元）之间有下列对应数据
回归方程为$\widehat{y}$=bx+a其中b=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$
（1）根据表中提供的数据，求出y与x的回归方程k；
（2）预测销售额为115万元时，大约需要多少万元广告费．
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
（1）根据表中提供的数据，求出y与x的回归方程k；
（2）预测销售额为115万元时，大约需要多少万元广告费．
11．在等差数列{an}中，a2+a5=19，S5=40，则a10=（ ）
| A． | 24 | B． | 27 | C． | 29 | D． | 48 |
18．已知正实数a，b满足a+b=3，则$\frac{1}{1+a}+\frac{4}{4+b}$的最小值为（ ）
| A． | 1 | B． | $\frac{7}{8}$ | C． | $\frac{9}{8}$ | D． | 2 |
8．在单调递增的等比数列{an}中，${a_{{1_{\;}}}}+{a_4}=5，{a_2}•{a_3}$=6，则$\frac{a_4}{a_1}$=（ ）
| A． | $\frac{2}{3}$ | B． | $\frac{3}{2}$ | C． | -$\frac{2}{3}$ | D． | -$\frac{3}{2}$ |
15．已知角$α∈（\frac{π}{2}，π）$，且tanα=-$\frac{{\sqrt{3}}}{3}$，则cosα的值为（ ）
| A． | $-\frac{{\sqrt{3}}}{3}$ | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
12．已知sinθ+cosθ=$\frac{4}{3}$（$\frac{π}{4}$＜θ＜$\frac{π}{2}$），则cosθ-sinθ的值为（ ）
| A． | $\frac{{\sqrt{2}}}{3}$ | B． | $-\frac{{\sqrt{2}}}{3}$ | C． | $\frac{1}{3}$ | D． | $-\frac{1}{3}$ |