题目内容
11.在等差数列{an}中,a2+a5=19,S5=40,则a10=( )| A. | 24 | B. | 27 | C. | 29 | D. | 48 |
分析 利用等差数列的通项公式与求和公式即可得出.
解答 解:设等差数列{an}的公差为d,∵a2+a5=19,S5=40,
∴2a1+5d=19,$5{a}_{1}+\frac{5×4}{2}$d=40,
解得a1=2,d=3.
则a10=2+9×3=29.
故选:C.
点评 本题考查了等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设θ为第二象限角,若tan(θ+$\frac{π}{4}$)=$\frac{1}{2}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $-\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
16.下列命题正确的个数是( )①已知p:?x∈R,方程ax2-2x+a=0有正实根,则¬p:?a∈R,方程ax2-2x+a=0有负实根
②?x∈R,x>0
③至少有一个整数,它既不是2的倍数,也不是3的倍数.
②?x∈R,x>0
③至少有一个整数,它既不是2的倍数,也不是3的倍数.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.双曲线$\frac{x^2}{5}-\frac{y^2}{4}=1$的( )
| A. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±\frac{{2\sqrt{5}}}{5}x$,离心率$e=\frac{{3\sqrt{5}}}{5}$ | |
| B. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±\frac{{\sqrt{5}}}{5}x$,离心率$e=\frac{9}{5}$ | |
| C. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±2\sqrt{5}x$,离心率$e=\frac{6}{5}$ | |
| D. | 实轴长为$2\sqrt{5}$,虚轴长为8,渐近线方程为$y=±\frac{{\sqrt{5}}}{2}x$,离心率$e=\frac{6}{5}$ |
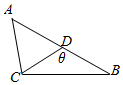 △ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.
△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{{\sqrt{3}sinC}}{cosB}=\frac{c}{b}$.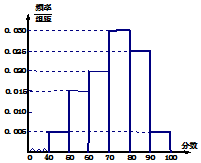 某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示: