题目内容
13.函数$f(x)=\left\{\begin{array}{l}{x^2}-2x-3,x≤0\\-2+lnx,x>0\end{array}\right.$的零点为-1或e2.分析 根据已知中函数$f(x)=\left\{\begin{array}{l}{x^2}-2x-3,x≤0\\-2+lnx,x>0\end{array}\right.$,分段求出各段上函数的零点,综合可得答案.
解答 解:当x≤0时,令x2-2x-3=0得:
x=-1,或x=3(舍去);
当x>0时,令-2+lnx=0得:
x=e2,
综上可得函数$f(x)=\left\{\begin{array}{l}{x^2}-2x-3,x≤0\\-2+lnx,x>0\end{array}\right.$的零点为:-1或e2,
故答案为:-1或e2
点评 本题考查的知识点是函数的零点的判定定理,分段函数的应用,分类讨论思想,难度基础.

练习册系列答案
相关题目
4.函数y=$\sqrt{1-x}+\sqrt{x}$的定义域为( )
| A. | (-∞,1] | B. | [0,1] | C. | [0,+∞) | D. | (-∞,0]∪[1,+∞) |
1.双曲线$\frac{x^2}{5}-\frac{y^2}{4}=1$的( )
| A. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±\frac{{2\sqrt{5}}}{5}x$,离心率$e=\frac{{3\sqrt{5}}}{5}$ | |
| B. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±\frac{{\sqrt{5}}}{5}x$,离心率$e=\frac{9}{5}$ | |
| C. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±2\sqrt{5}x$,离心率$e=\frac{6}{5}$ | |
| D. | 实轴长为$2\sqrt{5}$,虚轴长为8,渐近线方程为$y=±\frac{{\sqrt{5}}}{2}x$,离心率$e=\frac{6}{5}$ |
8.若复数z满足$z+i=\frac{2-i}{i}$,则复数z的模为( )
| A. | 10 | B. | $\sqrt{10}$ | C. | 4 | D. | $\sqrt{3}$ |
5.若偶函数f(x)在区间[-3,-1]上有最大值6,则f(x)在区间[1,3]上有( )
| A. | 最大值6 | B. | 最小值6 | C. | 最大值-6 | D. | 最小值-6 |
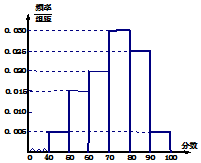 某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示: