题目内容
15.已知角$α∈(\frac{π}{2},π)$,且tanα=-$\frac{{\sqrt{3}}}{3}$,则cosα的值为( )| A. | $-\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 由已知求出角α,进一步求得cosα的值.
解答 解:∵$α∈(\frac{π}{2},π)$,且tanα=-$\frac{{\sqrt{3}}}{3}$,
∴α=$\frac{5π}{6}$,
则cosα=cos$\frac{5π}{6}$=$-\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查三角函数的化简求值,是基础的计算题.

练习册系列答案
相关题目
6.设θ为第二象限角,若tan(θ+$\frac{π}{4}$)=$\frac{1}{2}$,则sinθ+cosθ=( )
| A. | $-\frac{{\sqrt{10}}}{5}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $-\frac{{\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
7.已知两条不同的直线m,n和平面α,下列说法正确的是( )
| A. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n∥α | |
| B. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n与α相交 | |
| C. | 如果m∥α,n∥α,m、n共面,那么m∥n | |
| D. | 如果m?α,n∥α,m、n共面,那么m∥n |
4.函数y=$\sqrt{1-x}+\sqrt{x}$的定义域为( )
| A. | (-∞,1] | B. | [0,1] | C. | [0,+∞) | D. | (-∞,0]∪[1,+∞) |
5.若偶函数f(x)在区间[-3,-1]上有最大值6,则f(x)在区间[1,3]上有( )
| A. | 最大值6 | B. | 最小值6 | C. | 最大值-6 | D. | 最小值-6 |
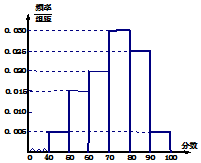 某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示: