题目内容
12.已知sinθ+cosθ=$\frac{4}{3}$($\frac{π}{4}$<θ<$\frac{π}{2}$),则cosθ-sinθ的值为( )| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $-\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
分析 利用同角三角函数的基本关系求得2sinθcosθ的值,再利用三角函数在各个象限中的符号,求得cosθ-sinθ=-$\sqrt{{(cosθ-sinθ)}^{2}}$ 的值.
解答 解:∵sinθ+cosθ=$\frac{4}{3}$($\frac{π}{4}$<θ<$\frac{π}{2}$),∴1+2sinθcosθ=$\frac{16}{9}$,
∴2sinθcosθ=$\frac{7}{9}$,
则cosθ-sinθ=-$\sqrt{{(cosθ-sinθ)}^{2}}$=-$\sqrt{1-2sinθcosθ}$=-$\frac{\sqrt{2}}{3}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系,以及三角函数在各个象限中的符号,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
7.已知两条不同的直线m,n和平面α,下列说法正确的是( )
| A. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n∥α | |
| B. | 如果m?α,n?α,m、n是不在任何同一个平面内的直线,那么n与α相交 | |
| C. | 如果m∥α,n∥α,m、n共面,那么m∥n | |
| D. | 如果m?α,n∥α,m、n共面,那么m∥n |
4.函数y=$\sqrt{1-x}+\sqrt{x}$的定义域为( )
| A. | (-∞,1] | B. | [0,1] | C. | [0,+∞) | D. | (-∞,0]∪[1,+∞) |
1.双曲线$\frac{x^2}{5}-\frac{y^2}{4}=1$的( )
| A. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±\frac{{2\sqrt{5}}}{5}x$,离心率$e=\frac{{3\sqrt{5}}}{5}$ | |
| B. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±\frac{{\sqrt{5}}}{5}x$,离心率$e=\frac{9}{5}$ | |
| C. | 实轴长为$2\sqrt{5}$,虚轴长为4,渐近线方程为$y=±2\sqrt{5}x$,离心率$e=\frac{6}{5}$ | |
| D. | 实轴长为$2\sqrt{5}$,虚轴长为8,渐近线方程为$y=±\frac{{\sqrt{5}}}{2}x$,离心率$e=\frac{6}{5}$ |
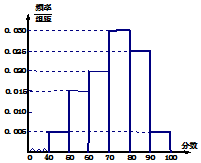 某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高三年级期末考试的学生中抽出20名学生,其成绩(均为整数)的频率分布直方图如图所示: