题目内容
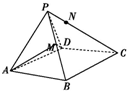 如图,已知△PAD是边长为2的等边三角形,且平面PAD⊥底面ABCD,其中四边形ABCD为菱形,且∠DAB=60°,点M为PB中点,N点在PC上,且CN=3PN.
如图,已知△PAD是边长为2的等边三角形,且平面PAD⊥底面ABCD,其中四边形ABCD为菱形,且∠DAB=60°,点M为PB中点,N点在PC上,且CN=3PN.(1)求证:PB⊥面ADM;
(2)求三棱锥N-ADM的体积.
考点:直线与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)取AD中点为Q,连结PQ,BQ.由已知得△PAD与△BAD都是边长为2的等边三角形,可证AD⊥面PQB,又PB?面PQB,可得PB⊥AD.又PB⊥AM,AM∩AD=A,即可证PB⊥面ADM.
(2)取PC中点为E,连结ME,则ME∥BC.又BC∥AD,所以ME∥AD,故A,D,E,M四点共面,又CN=3PN,所以N为PE中点,由三棱锥体积公式即可得解.
(2)取PC中点为E,连结ME,则ME∥BC.又BC∥AD,所以ME∥AD,故A,D,E,M四点共面,又CN=3PN,所以N为PE中点,由三棱锥体积公式即可得解.
解答:
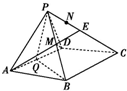 解:(1)取AD中点为Q,连结PQ,BQ.由已知可得△PAD与△BAD都是边长为2的等边三角形,
解:(1)取AD中点为Q,连结PQ,BQ.由已知可得△PAD与△BAD都是边长为2的等边三角形,
所以有AD⊥PQ,AD⊥BQ,又PQ∩BQ=Q⇒AD⊥面PQB.
又PB?面PQB,
∴PB⊥AD.
又PA=AB,PM=BM,所以有PB⊥AM,又AM∩AD=A,
∴PB⊥面ADM.(6分)
(2)取PC中点为E,连结ME,则ME∥BC.
又BC∥AD,所以ME∥AD,故A,D,E,M四点共面,
又CN=3PN,所以N为PE中点,
∴VN-ADM=
VP-ADM=
VM-PAD=
VB-PAD=
×
×
×4×
=
.(12分)
 解:(1)取AD中点为Q,连结PQ,BQ.由已知可得△PAD与△BAD都是边长为2的等边三角形,
解:(1)取AD中点为Q,连结PQ,BQ.由已知可得△PAD与△BAD都是边长为2的等边三角形,所以有AD⊥PQ,AD⊥BQ,又PQ∩BQ=Q⇒AD⊥面PQB.
又PB?面PQB,
∴PB⊥AD.
又PA=AB,PM=BM,所以有PB⊥AM,又AM∩AD=A,
∴PB⊥面ADM.(6分)
(2)取PC中点为E,连结ME,则ME∥BC.
又BC∥AD,所以ME∥AD,故A,D,E,M四点共面,
又CN=3PN,所以N为PE中点,
∴VN-ADM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 1 |
| 4 |
点评:本题主要考查了直线与平面垂直的判定,考查了三棱锥的体积的求法,考查了空间想象能力和转化思想,属于中档题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
已知平面向量
,
,|
|=2,
=(2,
),若|
-
|=
,则
在
上的投影为( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
运行如图所示的程序框图后,输出的结果是( )
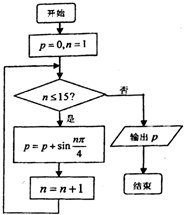

| A、0 | ||||
| B、1 | ||||
C、1+
| ||||
D、1+
|
