题目内容
解不等式:|2x-1|+|x+2|≥5.
考点:绝对值不等式的解法
专题:计算题,不等式的解法及应用,推理和证明
分析:把原不等式去掉绝对值,转化为与之等价的三个不等式组,分别求得每个不等式组的解集,再取并集,即得所求.
解答:
解:由不等式|2x-1|+|x+2|≥5,可得
①或
②或
③.
解①求得x∈∅,解②求得x∈∅,解③求得x≥
.
综上,不等式的解集为[
,+∞).
|
|
|
解①求得x∈∅,解②求得x∈∅,解③求得x≥
| 4 |
| 3 |
综上,不等式的解集为[
| 4 |
| 3 |
点评:本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知x,y∈R,且2x+3y>2-y+3-x,则下列各式中正确的是( )
| A、x-y>0 |
| B、x+y<0 |
| C、x-y<0 |
| D、x+y>0 |
函数f(x)是定义在R上的偶函数,且满足f(x+1)=f(x-1),当x∈[0,1]时,f(x)=2x,若方程ax+a-f(x)=0(a>0)恰有三个不相等的实数根,则实数a的取值范围是( )
A、(
| ||
| B、[0,2] | ||
| C、(1,2) | ||
| D、[1,+∞) |
某工厂生产甲、乙两种产品,每生产1吨甲产品需要用电2千度、用煤2吨、劳动力6人,产值为6千元;每生产1吨乙产品需要用电2千度、用煤4吨、劳动力3人,产值为7千元.但该厂每天的用电不得超过70千度、用煤不得超过120吨、劳动力不得超过180人.若该厂每天生产的甲、乙两种产品的数量分别为x、y(单位:吨),则该厂每天创造的最大产值z(单位:千元)为( )
| A、260 | B、235 |
| C、220 | D、210 |
在x轴、y轴上截距相等且与圆(x+2
)2+(y-3
)2=1相切的直线L共有( )条.
| 2 |
| 2 |
| A、2 | B、3 | C、4 | D、6 |
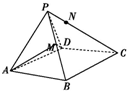 如图,已知△PAD是边长为2的等边三角形,且平面PAD⊥底面ABCD,其中四边形ABCD为菱形,且∠DAB=60°,点M为PB中点,N点在PC上,且CN=3PN.
如图,已知△PAD是边长为2的等边三角形,且平面PAD⊥底面ABCD,其中四边形ABCD为菱形,且∠DAB=60°,点M为PB中点,N点在PC上,且CN=3PN. 如图,在锐角三角形 A BC中,A B=2,点D在 BC边上,且AD=
如图,在锐角三角形 A BC中,A B=2,点D在 BC边上,且AD=