题目内容
已知平面向量
，
，|
|=2，
=（2，
），若|
-
|=
，则
在
上的投影为（ ）
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：平面向量数量积的运算
专题：平面向量及应用
分析：利用数量积运算性质可得
•
，再利用
在
上的投影=
，即可得出．
| a |
| b |
| a |
| b |
| ||||
|
|
解答：
解：∵
=（2，
），∴|
|=
．
∵|
|=2，|
-
|=
，
∴
=
，
∴4+7-2
•
=6，
∴
•
=
．
∴
在
上的投影=
=
=
．
故选：B．
| b |
| 3 |
| b |
| 7 |
∵|
| a |
| a |
| b |
| 6 |
∴
|
| 6 |
∴4+7-2
| a |
| b |
∴
| a |
| b |
| 5 |
| 2 |
∴
| a |
| b |
| ||||
|
|
| ||
|
5
| ||
| 14 |
故选：B．
点评：本题考查了数量积运算性质、向量的投影计算公式，考查了计算能力，属于基础题．
练习册系列答案
相关题目
|
| 1 |
| x |
A、e-
| ||
| B、1 | ||
| C、0 | ||
D、e
|
已知x，y∈R，且2x+3y＞2-y+3-x，则下列各式中正确的是（ ）
| A、x-y＞0 |
| B、x+y＜0 |
| C、x-y＜0 |
| D、x+y＞0 |
知双曲线
-
=1（a＞0，b＞0），A1、A2是实轴顶点，F是右焦点，B（0，b）是虚轴端点，若在线段BF上（不含端点）存在不同的两点Pi=（1，2），使得△PiA1A2（i=1，2）构成以A1A2为斜边的直角三角形，则双曲线离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（
| ||||||
B、（
| ||||||
C、（1，
| ||||||
D、（
|
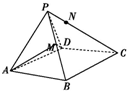如图，已知△PAD是边长为2的等边三角形，且平面PAD⊥底面ABCD，其中四边形ABCD为菱形，且∠DAB=60°，点M为PB中点，N点在PC上，且CN=3PN．