题目内容
求曲线y=-x2+2x+3的点到直线x-y+4=0的最短距离.
考点:直线与圆锥曲线的关系,点到直线的距离公式
专题:圆锥曲线的定义、性质与方程
分析:问题转化为平行线间的距离,联立直线与抛物线方程由△=0可得c值,可得距离.
解答:
解:平移直线x-y+4=0到与曲线y=-x2+2x+3相切可得直线l,
则直线x-y+4=0与直线l的距离即为所求最短距离,
由平行关系设l的方程为x-y+c=0,
联立
消去y并整理可得x2-x+c-3=0,
由相切可得△=(-1)2-4×1×(c-3)=0,解得c=
,
∴平行线间的距离d=
=
∴曲线y=-x2+2x+3的点到直线x-y+4=0的最短距离为
则直线x-y+4=0与直线l的距离即为所求最短距离,
由平行关系设l的方程为x-y+c=0,
联立
|
由相切可得△=(-1)2-4×1×(c-3)=0,解得c=
| 13 |
| 4 |
∴平行线间的距离d=
|
| ||
|
3
| ||
| 8 |
∴曲线y=-x2+2x+3的点到直线x-y+4=0的最短距离为
3
| ||
| 8 |
点评:本题考查距离公式,涉及直线与抛物线的相切问题,属中档题.

练习册系列答案
相关题目
某工厂生产甲、乙两种产品,每生产1吨甲产品需要用电2千度、用煤2吨、劳动力6人,产值为6千元;每生产1吨乙产品需要用电2千度、用煤4吨、劳动力3人,产值为7千元.但该厂每天的用电不得超过70千度、用煤不得超过120吨、劳动力不得超过180人.若该厂每天生产的甲、乙两种产品的数量分别为x、y(单位:吨),则该厂每天创造的最大产值z(单位:千元)为( )
| A、260 | B、235 |
| C、220 | D、210 |
在x轴、y轴上截距相等且与圆(x+2
)2+(y-3
)2=1相切的直线L共有( )条.
| 2 |
| 2 |
| A、2 | B、3 | C、4 | D、6 |
已知集合A={0,1},B={x∈R|
<0},则A∩B=( )
| x |
| x-2 |
| A、{0} | B、{1} |
| C、{0,1} | D、(0,1) |
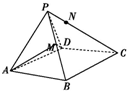 如图,已知△PAD是边长为2的等边三角形,且平面PAD⊥底面ABCD,其中四边形ABCD为菱形,且∠DAB=60°,点M为PB中点,N点在PC上,且CN=3PN.
如图,已知△PAD是边长为2的等边三角形,且平面PAD⊥底面ABCD,其中四边形ABCD为菱形,且∠DAB=60°,点M为PB中点,N点在PC上,且CN=3PN.