题目内容
若函数f（x）=-x2+x在[2，2+△x]（△x＞0）上的平均变化率不大于-1，求△x的范围．
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：利用平均变化率的意义即可得出．
解答：
解∵函数f（x）在区间[2，2+△x]上的增量△y=f（2+△x）-f（2）=-（△x+2）2+（△x+2）-（-22+2）=-△x2-3△x
∴f（x）在区间[2，2+△x]上上的平均变化率为
=-△x-3
∴-△x-3≤-1，
∴△x≥-2，
∵△x＞0，
∴△x的范围为（0，+∞）
∴f（x）在区间[2，2+△x]上上的平均变化率为
| △y |
| △x |
∴-△x-3≤-1，
∴△x≥-2，
∵△x＞0，
∴△x的范围为（0，+∞）
点评：本题考查了平均变化率的意义及其求法，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
，则f（x）的最小值为（ ）
|
| A、-4 | ||
| B、2 | ||
C、2
| ||
| D、4 |
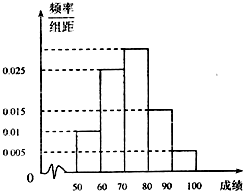国家教育部要求高中阶段每学年都要组织学生进行“国家学生体质健康数据测试”，方案要求以学校为单位组织实施，某校对高一1班同学按照“国家学生体质健康数据测试”项目按百分制进行了测试，并对50分以上的成绩进行统计，其频率分布直方图如图所示，若90～100分数段的人数为2人．已知函数f（x）定义域为[a，b]．则“函数f（x）在[a，b]上为单调函数”是“函数f（x）在[a，b]上有最大值和最小值”的（ ）
| A、充分但非必要条件 |
| B、必要但非充分条件 |
| C、充要条件 |
| D、既非充分也非必要条件 |
已知tan（α+β）=3，tan（α-β）=5，则tan（2α）的值为（ ）
A、-
| ||
B、
| ||
C、
| ||
D、-
|